Understanding probability is crucial in various fields, including mathematics, statistics, engineering, and even everyday decision-making. The concept of probability helps us quantify the likelihood of an event occurring. There are several approaches to finding probability, each suited to different scenarios and types of data. In this article, we'll explore five fundamental ways to calculate probability, providing a comprehensive overview of the methods, their applications, and the underlying principles.
Introduction to Probability Calculation
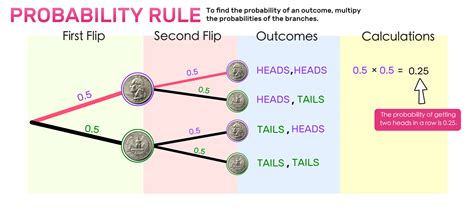
Probability is a measure of the likelihood that an event will occur. It is quantified as a number between 0 and 1, where 0 indicates that the event cannot occur and 1 indicates that the event will definitely occur. The calculation of probability can be approached in different ways, depending on the nature of the experiment or situation being analyzed. These methods include the classical approach, the relative frequency approach, the subjective approach, the empirical approach, and the axiomatic approach.
Key Points
- The classical approach to probability involves calculating the number of favorable outcomes divided by the total number of possible outcomes.
- The relative frequency approach estimates probability based on the proportion of times an event occurs in a long series of trials.
- The subjective approach to probability is based on personal belief or judgment about the likelihood of an event.
- The empirical approach involves using historical data to estimate probabilities.
- The axiomatic approach is based on a set of axioms or rules that define probability and is used in more theoretical and complex probability calculations.
The Classical Approach to Probability
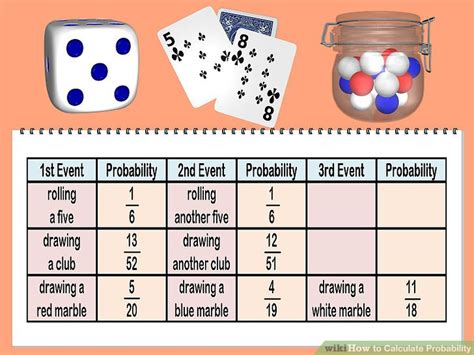
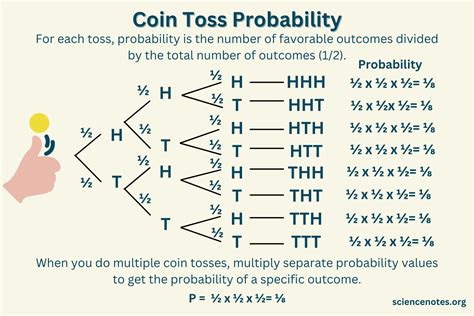
The classical approach, also known as the Laplace’s definition, is one of the oldest methods of calculating probability. It is used when all outcomes are equally likely. The formula for the classical probability of an event (E) is given by (P(E) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}). For example, if you roll a fair six-sided die, the probability of rolling a 4 is (\frac{1}{6}) because there is 1 favorable outcome (rolling a 4) out of 6 possible outcomes (rolling a 1, 2, 3, 4, 5, or 6).
Example of Classical Probability Calculation
In a deck of 52 cards, what is the probability of drawing a heart? Since there are 13 hearts in a deck of 52 cards, the probability is (P(\text{heart}) = \frac{13}{52} = \frac{1}{4}).
| Event | Number of Favorable Outcomes | Total Number of Possible Outcomes | Probability |
|---|---|---|---|
| Rolling a 4 on a die | 1 | 6 | 1/6 |
| Drawing a heart from a deck of cards | 13 | 52 | 1/4 |

The Relative Frequency Approach
The relative frequency approach to probability is based on the idea that the probability of an event is approximately equal to the proportion of times the event occurs in a long series of trials. This method is particularly useful when the classical approach cannot be applied due to unequal likelihoods of outcomes. The formula for the relative frequency probability is (P(E) = \frac{\text{Number of times event } E \text{ occurs}}{\text{Total number of trials}}). For instance, if a coin is flipped 1000 times and lands heads up 495 times, the relative frequency probability of getting heads is approximately (\frac{495}{1000} = 0.495).
Relative Frequency Example
A quality control engineer inspects 5000 units of a product and finds 125 defective units. The probability of a unit being defective, based on the relative frequency approach, is (P(\text{defective}) = \frac{125}{5000} = 0.025).
The Subjective Approach to Probability
The subjective approach to probability is based on an individual’s personal judgment or belief about the likelihood of an event. This approach is useful when there is limited data available or when the situation is unique and does not lend itself to statistical analysis. Subjective probabilities are often expressed as a range rather than a precise value, reflecting the uncertainty and variability in personal beliefs.
Subjective Probability Example
A farmer might estimate the probability of rain tomorrow based on his experience and current weather conditions. If he believes it is likely to rain but not certain, he might assign a subjective probability of 60% to 80% to the event of it raining tomorrow.
The Empirical Approach

The empirical approach to probability involves using historical data to estimate the likelihood of future events. This method is widely used in insurance, finance, and weather forecasting, among other fields. By analyzing past data, one can estimate the probability of an event occurring in the future, assuming that past trends will continue. For example, if historical data shows that a certain type of storm occurs once every 10 years, the empirical probability of such a storm occurring in any given year is approximately 0.1 or 10%.
Empirical Probability Calculation
A car insurance company finds that out of 10,000 policyholders, 500 were involved in accidents last year. The empirical probability of a policyholder being involved in an accident is (P(\text{accident}) = \frac{500}{10,000} = 0.05).
The Axiomatic Approach
The axiomatic approach to probability is based on a set of axioms or rules that define the properties of probability. This approach is more theoretical and provides a foundation for the mathematical treatment of probability. The three main axioms of probability are: (1) the probability of an event is a non-negative real number, (2) the probability of the certain event (the entire sample space) is 1, and (3) the probability of the union of mutually exclusive events is the sum of their probabilities. The axiomatic approach is crucial for deriving more complex probability distributions and for the study of probability theory in mathematics and statistics.
Axiomatic Approach Example
Given two mutually exclusive events (A) and (B), the probability of either (A) or (B) occurring is (P(A \cup B) = P(A) + P(B)), illustrating the third axiom of probability.
What is the difference between the classical and relative frequency approaches to probability?
+The classical approach assumes all outcomes are equally likely and calculates probability based on the number of favorable outcomes over the total number of outcomes. The relative frequency approach estimates probability based on the proportion of times an event occurs in a long series of trials, which is useful when outcomes are not equally likely.
How does the subjective approach to probability differ from the empirical approach?
+The subjective approach relies on personal judgment or belief about the likelihood of an event, whereas the empirical approach uses historical data to estimate probabilities. The subjective approach is more qualitative and can vary significantly from person to person, while the empirical approach is based on quantitative data and aims to provide a more objective estimate of probability.
In conclusion, the calculation of probability can be approached from different angles, each with its own set of assumptions and applications. Understanding these approaches is crucial for making informed decisions in various aspects of life, from personal choices to professional assessments. By applying the appropriate method based on the context and available data, individuals can better navigate uncertainty and make more accurate predictions about future events.