When dealing with complex functions, finding a local minimum can be a challenging task, especially in high-dimensional spaces. The goal is to identify a point where the function value is smaller than at neighboring points. This is crucial in various fields such as optimization, machine learning, and physics. In this article, we will delve into the world of local minima, exploring the concepts, methods, and techniques to find them efficiently.
Key Points
- Understanding the concept of local minima and its importance in optimization problems
- Overview of gradient-based methods for finding local minima, including gradient descent and its variants
- Introduction to Hessian matrix and its role in determining the nature of critical points
- Discussion on the choice of initial conditions and step sizes in iterative methods
- Exploration of advanced techniques, including quasi-Newton methods and trust-region methods
Introduction to Local Minima
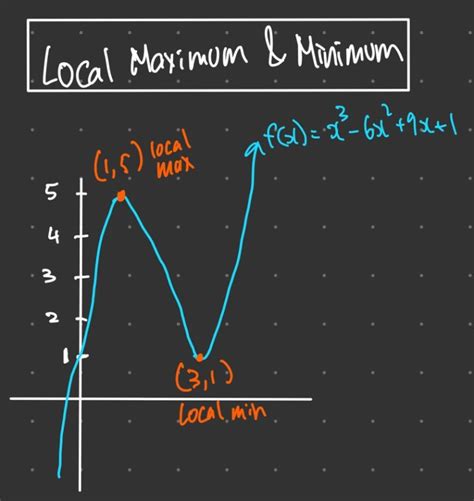
A local minimum of a function is a point where the function’s value is less than or equal to the values at nearby points. Formally, for a function f(x), a point x^* is a local minimum if there exists a neighborhood N of x^* such that f(x^*) \leq f(x) for all x \in N. The challenge lies in finding these points efficiently, especially when dealing with non-convex functions or high-dimensional spaces.
Gradient-Based Methods
One of the most common approaches to finding local minima is through gradient-based methods. The gradient of a function f(x) at a point x points in the direction of the steepest ascent. By moving in the opposite direction, we can iteratively converge to a local minimum. The basic gradient descent algorithm updates the current estimate x_k using the formula x_{k+1} = x_k - \alpha \nabla f(x_k), where \alpha is the step size and \nabla f(x_k) is the gradient of f at x_k.
| Method | Description |
|---|---|
| Gradient Descent | Basic iterative method using gradient for update |
| Stochastic Gradient Descent | Variant of gradient descent using stochastic approximation of the gradient |
| Conjugate Gradient | Method for solving systems of linear equations, useful for quadratic functions |
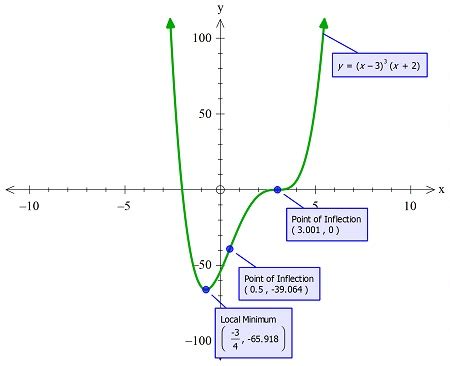
Advanced Techniques

Beyond basic gradient descent, several advanced techniques can be employed to find local minima more efficiently. The Hessian matrix, which contains the second partial derivatives of the function, provides valuable information about the curvature of the function and can be used to improve the convergence rate. Quasi-Newton methods, such as the BFGS algorithm, approximate the Hessian matrix using gradient information, offering a good balance between computational cost and convergence speed.
Trust-Region Methods
Trust-region methods offer another approach to finding local minima by iteratively solving a subproblem within a trust region around the current estimate. The trust region is a neighborhood where the model is trusted to be sufficiently accurate. By adjusting the size of the trust region based on the agreement between the model and the actual function values, these methods can adapt to the local geometry of the function, providing robust convergence.
For functions with multiple local minima, the choice of the initial condition can significantly influence the outcome of the optimization process. In such cases, techniques like simulated annealing or genetic algorithms can be useful, as they incorporate elements of randomness and exploration to escape local optima and potentially find the global minimum.
What is the main difference between a local and global minimum?
+A local minimum is a point where the function value is smaller than at neighboring points, while a global minimum is the point where the function achieves its lowest value across the entire domain.
How does the choice of step size affect the convergence of gradient descent?
+A step size that is too small can lead to slow convergence, while a step size that is too large can cause oscillations or divergence. An optimal step size balances these factors, ensuring stable and efficient convergence.
What is the role of the Hessian matrix in optimization?
+The Hessian matrix provides information about the second-order derivatives of the function, which can be used to determine the nature of critical points (whether they are minima, maxima, or saddle points) and to improve the convergence rate of optimization algorithms.
In conclusion, finding a local minimum quickly and efficiently is a complex task that requires a deep understanding of the underlying function and the optimization techniques available. By combining gradient-based methods with advanced techniques such as quasi-Newton methods and trust-region methods, and carefully considering the choice of initial conditions and step sizes, it is possible to develop robust and efficient optimization strategies tailored to specific problems.