Trigonometry, a branch of mathematics that deals with the relationships between the sides and angles of triangles, is a fundamental subject that has numerous applications in various fields, including physics, engineering, and navigation. Mastering trigonometry requires a deep understanding of its concepts, formulas, and theorems. Here are five essential tips to help you improve your trigonometry skills and become more proficient in solving trigonometric problems.
Key Points
- Understand the basics of trigonometry, including the definitions of sine, cosine, and tangent.
- Familiarize yourself with the unit circle and its relationship to trigonometric functions.
- Learn to apply trigonometric identities and formulas to simplify complex expressions and solve equations.
- Practice solving problems involving right triangles, including finding missing sides and angles.
- Develop your skills in graphing trigonometric functions and analyzing their properties.
Tip 1: Master the Basics of Trigonometry

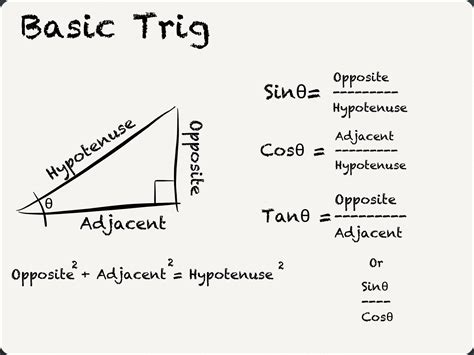
Before diving into advanced trigonometric concepts, it’s crucial to have a solid grasp of the basics. This includes understanding the definitions of sine, cosine, and tangent, as well as the relationships between these functions. The sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse, the cosine is the ratio of the length of the adjacent side to the length of the hypotenuse, and the tangent is the ratio of the length of the opposite side to the length of the adjacent side. These definitions are essential for solving problems involving right triangles.
Understanding the Unit Circle
The unit circle is a fundamental concept in trigonometry, and it’s essential to understand its relationship to trigonometric functions. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. The sine, cosine, and tangent of an angle can be defined in terms of the coordinates of a point on the unit circle. For example, the sine of an angle is equal to the y-coordinate of the point where the terminal side of the angle intersects the unit circle. Understanding the unit circle and its properties can help you visualize and solve trigonometric problems more effectively.
| Trigonometric Function | Definition |
|---|---|
| Sine (sin) | Opposite side / Hypotenuse |
| Cosine (cos) | Adjacent side / Hypotenuse |
| Tangent (tan) | Opposite side / Adjacent side |
Tip 2: Apply Trigonometric Identities and Formulas

Trigonometric identities and formulas are essential tools for simplifying complex expressions and solving equations. Some of the most commonly used identities include the Pythagorean identity (sin^2(x) + cos^2(x) = 1), the sum and difference formulas for sine and cosine, and the double-angle formulas. These identities can help you simplify expressions, solve equations, and prove trigonometric statements. For example, you can use the Pythagorean identity to find the value of sin(x) given the value of cos(x), or use the sum and difference formulas to find the value of sin(x + y) given the values of sin(x) and sin(y).
Practicing with Right Triangles
Right triangles are a fundamental concept in trigonometry, and practicing with them can help you develop your problem-solving skills. You can start by finding the lengths of missing sides and angles in right triangles, using the definitions of sine, cosine, and tangent. As you become more proficient, you can move on to more complex problems, such as finding the area of a triangle given the lengths of two sides and the included angle, or finding the length of a side given the area and the lengths of the other two sides.
Some of the key concepts to focus on when practicing with right triangles include the 30-60-90 triangle, the 45-45-90 triangle, and the Pythagorean theorem. These concepts can help you solve problems more efficiently and develop your critical thinking skills. For example, you can use the 30-60-90 triangle to find the length of the hypotenuse of a right triangle given the length of the shorter leg, or use the Pythagorean theorem to find the length of the hypotenuse given the lengths of the other two sides.
Tip 3: Graph Trigonometric Functions
Graphing trigonometric functions is an essential skill in trigonometry, as it can help you visualize and analyze the properties of these functions. The graph of a trigonometric function can provide valuable information about its behavior, including its amplitude, period, and phase shift. You can use graphing calculators or software to visualize the graphs of trigonometric functions and explore their properties. For example, you can graph the sine function to see its periodic behavior, or graph the cosine function to see its relationship to the sine function.
Analyzing Trigonometric Functions
Once you’ve graphed a trigonometric function, you can analyze its properties to gain a deeper understanding of its behavior. Some of the key properties to focus on include the amplitude, period, and phase shift of the function. The amplitude of a trigonometric function is the maximum value it attains, the period is the distance between two consecutive points on the graph that have the same y-value, and the phase shift is the horizontal translation of the graph. By analyzing these properties, you can develop a better understanding of the behavior of trigonometric functions and how they can be used to model real-world phenomena.
What is the definition of the sine function?
+The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
How do I find the length of a missing side in a right triangle?
+You can use the Pythagorean theorem to find the length of a missing side in a right triangle, given the lengths of the other two sides.
What is the relationship between the sine and cosine functions?
+The sine and cosine functions are related by the Pythagorean identity: sin^2(x) + cos^2(x) = 1.
By following these five tips and practicing regularly, you can develop a deep understanding of trigonometry and become proficient in solving trigonometric problems. Remember to start with the basics, practice with right triangles, apply trigonometric identities and formulas, graph trigonometric functions, and analyze their properties. With time and effort, you can master the concepts and techniques of trigonometry and apply them to a wide range of problems in mathematics, science, and engineering.