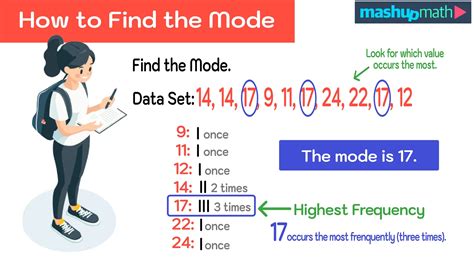
Understanding statistical concepts is essential in data analysis, and one of the key measures of central tendency is the mode. The mode is the value that appears most frequently in a data set. It is a crucial concept in statistics and is used in various fields, including business, economics, and social sciences. In this article, we will explore five ways to calculate the mode, including its application in real-world scenarios.
Key Points
- The mode is the value that appears most frequently in a data set.
- There are different types of modes, including unimodal, bimodal, and multimodal distributions.
- The mode can be calculated using various methods, including the manual count method, the histogram method, and the graphical method.
- Technology, such as calculators and computer software, can also be used to calculate the mode.
- Understanding the mode is essential in data analysis, as it provides valuable insights into the characteristics of a data set.
What is the Mode?

The mode is a measure of central tendency that represents the value that appears most frequently in a data set. It is an essential concept in statistics, as it provides valuable insights into the characteristics of a data set. The mode can be used to identify patterns and trends in data, and it is often used in conjunction with other measures of central tendency, such as the mean and median.
Types of Modes
There are different types of modes, including unimodal, bimodal, and multimodal distributions. A unimodal distribution has one mode, while a bimodal distribution has two modes. A multimodal distribution has more than two modes. Understanding the type of mode in a data set is essential, as it can provide valuable insights into the characteristics of the data.
5 Ways to Calculate the Mode

There are various ways to calculate the mode, including:
1. Manual Count Method
The manual count method involves counting the frequency of each value in a data set to determine the mode. This method is simple and straightforward but can be time-consuming for large data sets.
2. Histogram Method
The histogram method involves creating a histogram of the data set and identifying the value with the highest frequency. This method is useful for visualizing the distribution of the data and identifying the mode.
3. Graphical Method
The graphical method involves creating a graph of the data set and identifying the value with the highest frequency. This method is similar to the histogram method but uses a different type of graph.
4. Calculator Method
The calculator method involves using a calculator to calculate the mode. This method is quick and easy but requires a calculator with statistical functions.
5. Computer Software Method
The computer software method involves using computer software, such as Excel or SPSS, to calculate the mode. This method is quick and easy but requires access to computer software with statistical functions.
| Method | Description |
|---|---|
| Manual Count Method | Counting the frequency of each value in a data set |
| Histogram Method | Creating a histogram of the data set and identifying the value with the highest frequency |
| Graphical Method | Creating a graph of the data set and identifying the value with the highest frequency |
| Calculator Method | Using a calculator to calculate the mode |
| Computer Software Method | Using computer software to calculate the mode |
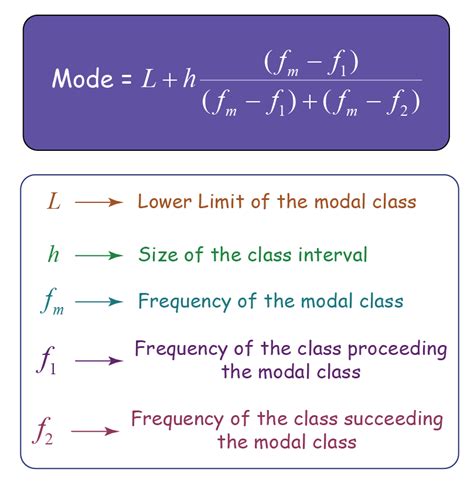
Real-World Applications of the Mode
The mode has various real-world applications, including business, economics, and social sciences. For example, a company may use the mode to identify the most popular product or service, while an economist may use the mode to identify the most common income level in a population. The mode is also used in social sciences to identify patterns and trends in data.
Example of the Mode in Business
A company that sells shoes may use the mode to identify the most popular shoe size. By analyzing the data, the company may find that the most popular shoe size is 8. This information can be used to inform production and inventory decisions, ensuring that the company has enough stock of the most popular shoe size.
Example of the Mode in Economics
An economist may use the mode to identify the most common income level in a population. By analyzing the data, the economist may find that the most common income level is $50,000. This information can be used to inform policy decisions, such as determining the optimal tax rate or identifying areas where government support may be needed.
What is the mode, and why is it important in statistics?
+The mode is the value that appears most frequently in a data set. It is important in statistics because it provides valuable insights into the characteristics of a data set and can be used to identify patterns and trends.
How do I calculate the mode using the manual count method?
+To calculate the mode using the manual count method, count the frequency of each value in the data set and identify the value with the highest frequency.
What are the advantages and disadvantages of using the mode as a measure of central tendency?
+The mode is a useful measure of central tendency because it is easy to calculate and understand. However, it can be affected by outliers and may not provide a complete picture of the data set.
In conclusion, the mode is a crucial concept in statistics that provides valuable insights into the characteristics of a data set. By understanding the mode and how to calculate it, individuals can gain a deeper understanding of their data and make informed decisions. The five methods outlined above, including the manual count method, histogram method, graphical method, calculator method, and computer software method, can be used to calculate the mode. The mode has various real-world applications, including business, economics, and social sciences, and is an essential tool for anyone working with data.