Converting units of measurement is a fundamental aspect of various fields, including mathematics, physics, and engineering. One common conversion is from yards to feet, as both units are used to measure length or distance. To understand the conversion process, it's essential to know the relationship between yards and feet. There are 3 feet in a yard, which serves as the basis for converting between these two units.
Understanding the Conversion Factor
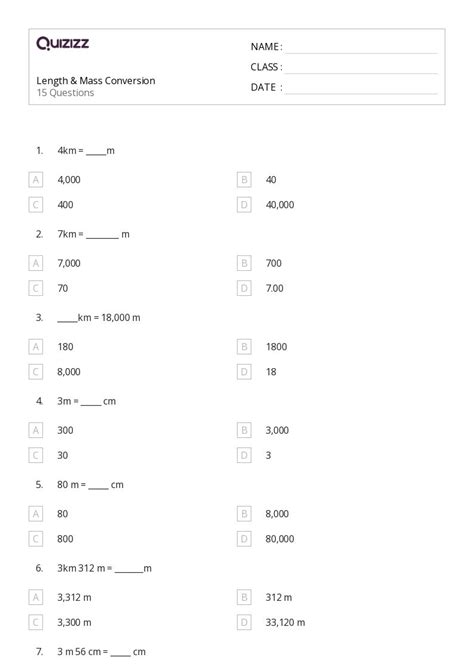
The conversion factor between yards and feet is straightforward: 1 yard equals 3 feet. This factor can be used to convert any number of yards to feet by multiplying the number of yards by 3. For example, to convert 100 yards to feet, you would multiply 100 by 3, resulting in 300 feet. This simple multiplication process makes conversions between these units relatively easy.
Converting 300 Yards to Feet
To convert 300 yards to feet, apply the conversion factor: multiply 300 yards by 3 feet per yard. The calculation is as follows: 300 yards * 3 feet/yard = 900 feet. Therefore, 300 yards is equivalent to 900 feet.
| Unit | Conversion Factor | Result |
|---|---|---|
| 300 Yards | 3 Feet/Yard | 900 Feet |

Key Points
- The conversion factor from yards to feet is 3 feet per yard.
- To convert yards to feet, multiply the number of yards by 3.
- 300 yards is equivalent to 900 feet when converted using the factor of 3 feet per yard.
- Accurate conversions between units of measurement are critical in various professional and practical applications.
- Understanding the relationship between different units of measurement facilitates more effective problem-solving and calculation in fields requiring precise measurements.
Practical Applications of Unit Conversion

Unit conversions are not limited to theoretical mathematics; they have real-world implications in fields like architecture, engineering, and physics. For instance, an architect designing a building must ensure that all measurements are accurate and consistent, whether working in yards, feet, or other units. Incorrect conversions can lead to costly mistakes, such as incorrectly sized materials or flawed structural designs.
Importance of Precision in Measurement
Precision in measurement and conversion is vital to avoid errors. In scientific research, small discrepancies in measurement can significantly affect the outcome of experiments and the validity of conclusions drawn from the data. Similarly, in construction, precise measurements ensure that structures are built safely and according to plan, reducing the risk of accidents or building failures.
| Field | Importance of Precision |
|---|---|
| Construction | Ensures safety and structural integrity of buildings. |
| Scientific Research | Affects the validity and reliability of experimental results. |
| Engineering | Critical for the design and functioning of mechanical systems and infrastructures. |
Conclusion and Future Implications
In conclusion, converting 300 yards to feet involves a simple yet critical mathematical operation that yields 900 feet. This conversion, like others, underscores the importance of precision and understanding in unit measurements. As technology advances and global communication increases, the need for accurate and consistent measurements will only grow, making the fundamentals of unit conversion more relevant than ever.
Why is precision in unit conversion important?
+Precision in unit conversion is crucial because it affects the accuracy of calculations, designs, and outcomes in various fields, including construction, scientific research, and engineering. Small errors can lead to significant discrepancies, potentially causing safety issues, financial losses, or invalid research findings.
How do you convert yards to feet?
+To convert yards to feet, you multiply the number of yards by 3, since there are 3 feet in a yard. For example, to convert 300 yards to feet, you calculate 300 * 3 = 900 feet.
What are some real-world applications of unit conversion?
+Unit conversion has numerous real-world applications, including architectural design, engineering projects, scientific experiments, and everyday measurements. Accurate conversions ensure that designs are feasible, experiments are valid, and constructions are safe and functional.
As the world becomes increasingly interconnected, the importance of accurate measurements and conversions will continue to grow, necessitating a deep understanding of unit conversion principles and their practical applications.



