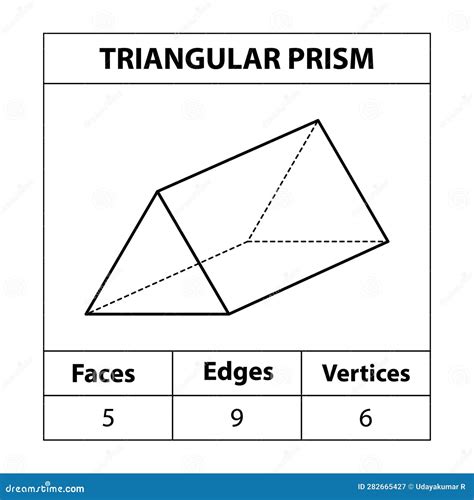
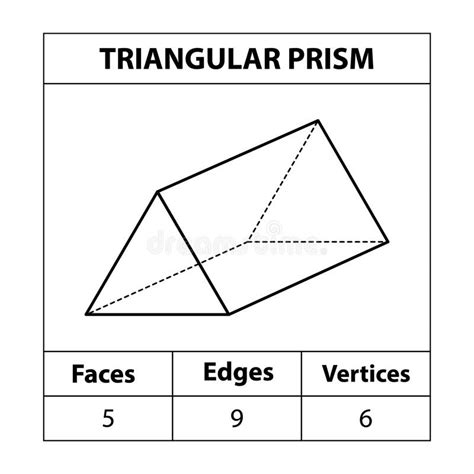
A triangular prism is a three-dimensional solid object that has two identical faces that are triangles, and three rectangular faces that connect the corresponding sides of the triangles. The correct number of faces of a triangular prism is 5, consisting of 2 triangular faces and 3 rectangular faces. This fundamental concept in geometry is crucial for understanding various spatial relationships and calculations involving volume, surface area, and other properties of triangular prisms.
Key Points
- A triangular prism has 5 faces in total.
- It includes 2 triangular faces that are identical.
- There are 3 rectangular faces connecting the sides of the triangles.
- Understanding the structure of a triangular prism is essential for geometry and spatial calculations.
- The number of faces is a basic property used in various geometric analyses.
Structural Components of a Triangular Prism
A triangular prism’s structure is composed of its faces, edges, and vertices. Each face of the prism is a flat surface, with the two triangular faces being the bases and the three rectangular faces being the lateral faces. The edges are the lines where two faces meet, and the vertices are the points where three or more edges intersect. The number and arrangement of these components are critical in defining the geometric properties of the prism.
Properties of Triangular Prisms
Triangular prisms have several notable properties. The volume of a triangular prism can be calculated by multiplying the area of one of its triangular bases by its height (the distance between the two bases). The surface area is the sum of the areas of all its faces. The relationship between the dimensions of the triangular bases and the height of the prism influences its overall dimensions and spatial properties.
| Property | Description |
|---|---|
| Number of Faces | 5 faces (2 triangular, 3 rectangular) |
| Number of Edges | 9 edges |
| Number of Vertices | 6 vertices |
Applications of Triangular Prisms
Triangular prisms are used in various real-world applications due to their unique properties. In architecture, they are used in the design of roofs, bridges, and other structures where a strong, stable shape is required. In engineering, the calculation of stress and strain on triangular prism structures is crucial for ensuring safety and durability. Moreover, in product design, the triangular prism shape can offer advantages in terms of stability and spatial efficiency.
Calculating Volume and Surface Area
The volume (V) of a triangular prism is given by the formula (V = A \times h), where (A) is the area of one of the triangular bases and (h) is the height of the prism. The area of a triangle can be calculated using the formula (A = \frac{1}{2} \times b \times l), where (b) is the base of the triangle and (l) is its height. The surface area of the prism is the sum of the areas of its 5 faces, which includes the two triangular bases and the three rectangular lateral faces.
For a triangular prism with a base triangle of sides 5 cm and 6 cm, and a height of 10 cm, the volume would be calculated as follows: First, find the area of the base triangle, which is \frac{1}{2} \times 5 \times 6 = 15 square cm. Then, multiply this area by the height of the prism, 15 \times 10 = 150 cubic cm.
What is the formula for the volume of a triangular prism?
+The formula for the volume of a triangular prism is V = A \times h, where A is the area of the triangular base and h is the height of the prism.
How do you calculate the surface area of a triangular prism?
+The surface area of a triangular prism is calculated by adding the areas of its 5 faces: the two triangular bases and the three rectangular faces.
What are some real-world applications of triangular prisms?
+Triangular prisms are used in architecture for designing roofs and bridges, in engineering for calculating stress and strain, and in product design for creating stable and spatially efficient structures.
In conclusion, the triangular prism, with its 5 faces, offers a unique combination of structural stability and spatial efficiency, making it a fundamental shape in geometry and various practical applications. Understanding its properties, such as volume and surface area, is essential for solving geometric problems and designing structures in engineering and architecture.