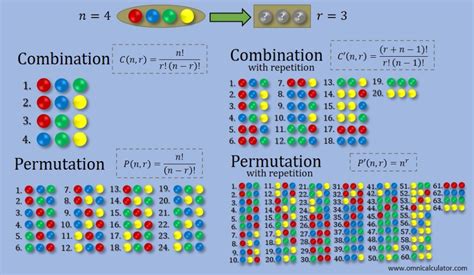
The concept of combinations is a fundamental aspect of combinatorial mathematics, dealing with the selection of items from a larger set, without regard to the order of selection. When we talk about combinations of 4 numbers, we are essentially discussing the various ways in which 4 numbers can be chosen from a larger set, such as the set of natural numbers, integers, or any other defined numerical set. This concept has numerous applications in statistics, probability theory, and computer science, among other fields.
Understanding Combinations

Combinations are distinct from permutations in that the order of selection does not matter. For instance, if we are choosing 4 numbers from a set of 10, the combination (1, 2, 3, 4) is the same as (4, 3, 2, 1) because the order of the numbers does not change the fact that the same 4 numbers are selected. The formula for calculating combinations is given by C(n, k) = n! / [k!(n-k)!], where n is the total number of items, k is the number of items to choose, and “!” denotes factorial, the product of all positive integers up to that number.
Calculating Combinations of 4 Numbers
To calculate the number of combinations of 4 numbers from a set of n numbers, we use the combination formula. For example, if we want to find the number of ways to choose 4 numbers out of 10, we calculate C(10, 4) = 10! / [4!(10-4)!] = 10! / (4!6!) = 210. This means there are 210 different combinations of 4 numbers that can be chosen from a set of 10 numbers.
| Set Size (n) | Number of Items to Choose (k) | Number of Combinations |
|---|---|---|
| 10 | 4 | 210 |
| 20 | 4 | 4845 |
| 30 | 4 | 27405 |

Applications of Combinations

Combinations have a wide range of applications. In probability theory, they are used to calculate the number of favorable outcomes for certain events. In computer science, combinations are used in algorithms for solving complex problems, such as the traveling salesman problem. In statistics, combinations are crucial for understanding sampling distributions and making inferences about populations.
Real-World Examples
A real-world example of combinations in action is in lottery systems. When players choose 4 numbers out of 49 (a common setup in many lottery games), the number of possible combinations is calculated using the combination formula, which helps in understanding the odds of winning. Another example is in committee selection, where a group of 4 members needs to be chosen from a larger group of 20, and the number of possible combinations of committees can be calculated.
Key Points
- The combination formula C(n, k) = n! / [k!(n-k)!] is used to calculate the number of ways to choose k items from a set of n items without regard to the order.
- Combinations have numerous applications in mathematics, statistics, computer science, and real-world problems.
- Understanding combinations is crucial for calculating probabilities, solving complex problems, and making informed decisions.
- The size of the set (n) and the number of items to choose (k) significantly affect the number of combinations.
- Real-world applications include lottery systems, committee selections, and statistical analysis.
Conclusion and Future Directions
In conclusion, combinations of 4 numbers represent a fundamental concept in combinatorial mathematics with widespread applications. The ability to calculate and understand combinations is vital for solving problems in various fields. As computational power increases and data analysis becomes more sophisticated, the importance of combinatorial principles, including combinations, will continue to grow. Further research and development in this area will lead to new methodologies and tools for tackling complex problems in science, technology, and beyond.
What is the difference between permutations and combinations?
+Permutations consider the order of selection, while combinations do not. For example, in permutations, (1, 2, 3) and (3, 2, 1) are considered different, but in combinations, they are the same because the order does not matter.
How are combinations used in real-world applications?
+Combinations are used in lottery systems to calculate the odds of winning, in committee selections to determine the number of possible committees, and in statistical analysis to understand sampling distributions and make inferences about populations.
What is the formula for calculating combinations?
+The formula for calculating combinations is C(n, k) = n! / [k!(n-k)!], where n is the total number of items, k is the number of items to choose, and “!” denotes factorial.