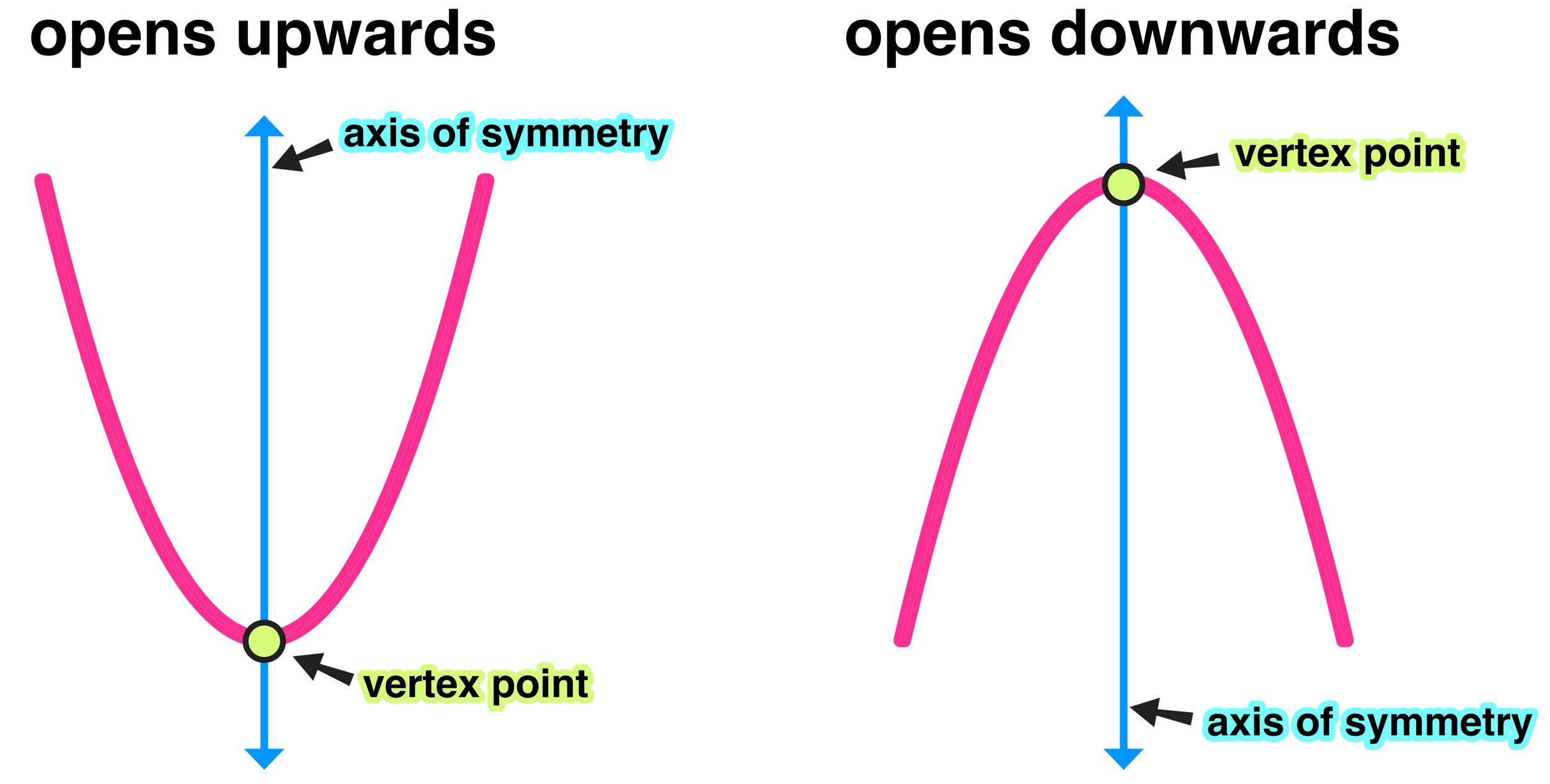
The vertex of a parabola is the lowest or highest point on the parabola, depending on its orientation. Finding the vertex is crucial in understanding the behavior and properties of the parabola. In this article, we will explore how to find the vertex of a parabola easily, using both the standard form of a quadratic equation and the vertex form.
Key Points
- The standard form of a quadratic equation is ax^2 + bx + c, where a, b, and c are constants.
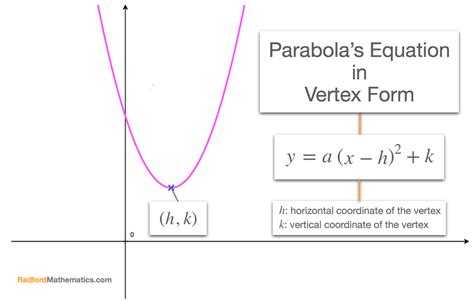
- The vertex form of a parabola is y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola.
- To find the vertex from the standard form, we use the formula h = -\frac{b}{2a} and then substitute h back into the equation to find k.
- Understanding the vertex helps in analyzing the parabola's position, direction, and intercepts.
- Real-world applications of finding the vertex include optimization problems in physics, engineering, and economics.
Understanding Parabolas and Their Vertex
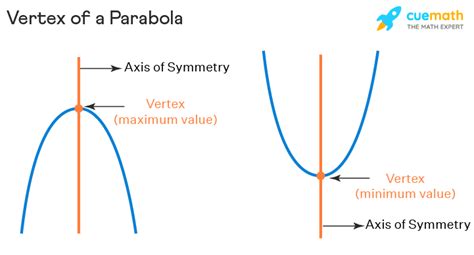
A parabola is a U-shaped curve that opens upwards or downwards. The vertex is the point where the parabola changes direction. For a parabola that opens upwards, the vertex is the lowest point, while for one that opens downwards, it is the highest point. The equation of a parabola can be given in the standard form (y = ax^2 + bx + c), where (a), (b), and (c) are constants, and (a) determines the direction the parabola opens.
Converting to Vertex Form
The vertex form of a parabola is (y = a(x - h)^2 + k), where ((h, k)) is the vertex. To find the vertex from the standard form, we need to convert the equation into vertex form. The (x)-coordinate of the vertex, (h), can be found using the formula (h = -\frac{b}{2a}). Once (h) is known, we can substitute it back into the standard form of the equation to find (k), the (y)-coordinate of the vertex.
| Step | Description |
|---|---|
| 1 | Identify the coefficients a, b, and c in the standard form y = ax^2 + bx + c. |
| 2 | Calculate h = -\frac{b}{2a} to find the x-coordinate of the vertex. |
| 3 | Substitute h back into the equation y = ax^2 + bx + c to find k, the y-coordinate of the vertex. |
| 4 | The vertex of the parabola is (h, k). |
Applications and Examples

Finding the vertex of a parabola has numerous real-world applications. In physics, the trajectory of a projectile under the influence of gravity can be modeled as a parabola, with the vertex representing the maximum height reached. In economics, parabolas can model cost or revenue functions, where the vertex might represent a minimum or maximum value. Understanding how to find the vertex efficiently is crucial for solving these problems.
Example Calculation
Consider the parabola given by (y = 2x^2 + 4x + 1). To find the vertex, first calculate (h = -\frac{b}{2a} = -\frac{4}{2*2} = -1). Then, substitute (x = -1) into the equation to find (k): (y = 2(-1)^2 + 4(-1) + 1 = 2 - 4 + 1 = -1). Thus, the vertex is ((-1, -1)).
In conclusion, finding the vertex of a parabola is a straightforward process that involves converting the standard form of a quadratic equation into vertex form. By understanding the formula h = -\frac{b}{2a} and how to substitute h back into the equation to find k, one can easily identify the vertex of any parabola given in standard form. This skill is not only essential in algebra but also has practical applications across various disciplines.
What is the importance of finding the vertex of a parabola?
+Finding the vertex is crucial for understanding the parabola’s orientation, position, and key features such as maxima or minima, which are essential in various mathematical and real-world applications.
How does the value of (a) affect the parabola?
+The value of (a) determines the direction the parabola opens. If (a > 0), the parabola opens upwards; if (a < 0), it opens downwards. The magnitude of (a) affects how wide or narrow the parabola is.
Can the vertex form be used for all types of quadratic equations?
+Yes, the vertex form (y = a(x - h)^2 + k) can represent any quadratic equation. It’s particularly useful for identifying the vertex and analyzing the parabola’s shape and position.