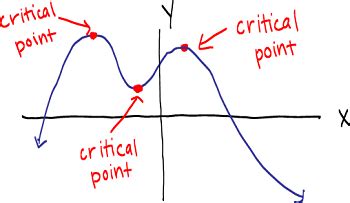
Identifying critical points is a crucial step in various mathematical and real-world applications, including optimization problems, physics, and engineering. Critical points are where the function's derivative is zero or undefined, indicating a possible maximum, minimum, or point of inflection. Here, we'll explore five ways to find critical points, each with its own strengths and applications.
Understanding the Concept of Critical Points
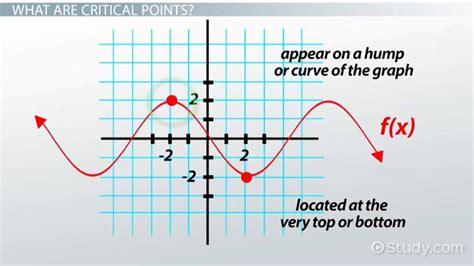
Critical points are fundamental in calculus, serving as the foundation for understanding how functions behave. They can be found using various methods, each suited to different types of functions and applications. The concept of critical points extends beyond mathematics, with applications in fields like economics, where they can represent equilibrium points, and in physics, where they can indicate phase transitions.
1. Finding Critical Points Using Derivatives
The most straightforward method to find critical points is by calculating the derivative of a function and setting it equal to zero. This method is based on the fact that at critical points, the slope of the tangent line to the function is zero (for maxima or minima) or undefined (for points of inflection). For a function f(x), we find its derivative f’(x) and solve the equation f’(x) = 0 for x. This method is widely applicable but requires the function to be differentiable.
| Function | Derivative | Critical Points |
|---|---|---|
| f(x) = x^2 | f'(x) = 2x | x = 0 |
| f(x) = 3x^2 + 2x - 5 | f'(x) = 6x + 2 | x = -1/3 |

2. Using the Second Derivative Test
After finding critical points, the second derivative test can be used to determine whether these points correspond to local maxima, minima, or neither. This involves calculating the second derivative of the function, f”(x), and evaluating its sign at the critical points. If f”(x) > 0, the critical point is a local minimum; if f”(x) < 0, it’s a local maximum; and if f”(x) = 0, the test is inconclusive. This method provides additional insight into the nature of critical points.
Practical Applications of Critical Points

Critical points have numerous practical applications. In physics, they can represent the points where a force acting on an object is balanced by another force, leading to equilibrium. In economics, critical points can signify market equilibrium, where the supply of a good equals its demand. Understanding and identifying these points is essential for predicting and analyzing the behavior of complex systems.
3. Numerical Methods for Finding Critical Points
For functions where analytical differentiation is challenging or impossible, numerical methods can be employed to approximate critical points. These methods, such as the Newton-Raphson method or gradient descent, iteratively refine an initial guess for the critical point until convergence. Numerical methods are particularly useful for complex functions or when dealing with experimental data.
4. Graphical Analysis
A more visual approach to finding critical points involves graphing the function and identifying points where the function changes from increasing to decreasing (local maxima) or from decreasing to increasing (local minima). This method, while not as precise as analytical or numerical methods, provides a quick and intuitive way to identify critical points, especially for simple functions.
5. Using Software and Computational Tools
With the advent of computational software like Mathematica, MATLAB, or Python libraries such as NumPy and SciPy, finding critical points has become significantly easier. These tools can symbolically differentiate functions, solve equations numerically, and even graph functions, making the process of identifying critical points more efficient and less prone to human error.
Key Points
- Critical points are found where a function's derivative is zero or undefined.
- The second derivative test can determine if a critical point is a local maximum or minimum.
- Numerical methods are useful for complex functions or experimental data.
- Graphical analysis provides a visual method for identifying critical points.
- Computational tools can significantly simplify the process of finding and analyzing critical points.
In conclusion, identifying critical points is a multifaceted problem with various approaches, each suited to different contexts and applications. Whether through derivatives, numerical methods, graphical analysis, or computational tools, understanding critical points is essential for analyzing and optimizing functions in mathematics, physics, engineering, and beyond.
What are critical points in a function?
+Critical points are where the derivative of a function is zero or undefined, indicating possible maxima, minima, or points of inflection.
How do you find critical points using derivatives?
+Find the derivative of the function and set it equal to zero. Solve the resulting equation for x to find the critical points.
What is the purpose of the second derivative test?
+The second derivative test determines whether a critical point is a local maximum, minimum, or neither, based on the sign of the second derivative at the critical point.