Asymptotes are fundamental concepts in mathematics, particularly in calculus and algebra, representing lines that a graph approaches but never touches. Finding asymptotes is crucial for understanding the behavior of functions, especially as the input or output values tend towards infinity or negative infinity. There are several types of asymptotes, including vertical, horizontal, and oblique (or slant) asymptotes. Here, we'll delve into five ways to find asymptotes, exploring both the theoretical foundations and practical applications of these methods.
Key Points
- Identifying vertical asymptotes through denominator analysis in rational functions
- Determining horizontal asymptotes by comparing degrees of polynomials in the numerator and denominator
- Discovering oblique asymptotes through polynomial long division or synthetic division
- Using limits to confirm the presence and equations of asymptotes
- Graphical analysis for visual identification and approximation of asymptotes
Understanding Asymptotes: A Foundation

Before diving into the methods for finding asymptotes, it’s essential to understand what asymptotes represent. Asymptotes are lines that the graph of a function approaches as the absolute value of the x-coordinate gets larger and larger. The three main types of asymptotes are vertical, horizontal, and oblique. Vertical asymptotes occur where the function is undefined, typically due to division by zero in rational functions. Horizontal asymptotes are determined by the behavior of the function as x approaches infinity or negative infinity, often influenced by the degrees of the polynomials in the numerator and denominator. Oblique or slant asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator, resulting in a linear function that the graph approaches.
1. Identifying Vertical Asymptotes
Vertical asymptotes are found by setting the denominator of a rational function equal to zero and solving for x. This is because a rational function is undefined when its denominator equals zero, leading to a vertical asymptote at that x-value. For example, in the function f(x) = 1 / (x - 2), setting the denominator x - 2 = 0 gives x = 2 as a vertical asymptote. It’s crucial to ensure that any common factors between the numerator and denominator are canceled out before identifying vertical asymptotes, as these cancellations can eliminate potential asymptotes.
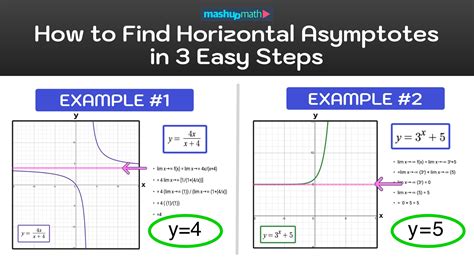
2. Determining Horizontal Asymptotes
Horizontal asymptotes are determined by comparing the degrees of the polynomials in the numerator and the denominator of a rational function. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0. If the degrees are equal, the horizontal asymptote is the ratio of the leading coefficients. For instance, in the function f(x) = (2x^2 + 3x) / (x^2 + 1), since the degrees of the numerator and denominator are equal, the horizontal asymptote is y = 2⁄1 = 2. If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote, but there might be an oblique asymptote.
| Type of Asymptote | Conditions |
|---|---|
| Vertical | Denominator equals zero |
| Horizontal | Degree of numerator less than or equal to degree of denominator |
| Oblique | Degree of numerator exactly one more than degree of denominator |

3. Discovering Oblique Asymptotes
Oblique or slant asymptotes occur when the degree of the numerator is exactly one greater than the degree of the denominator in a rational function. To find an oblique asymptote, one can perform polynomial long division or synthetic division. For example, in the function f(x) = (x^2 + 2x + 1) / x, performing polynomial long division yields f(x) = x + 2 + 1/x. The oblique asymptote is the non-remainder part of the result, which is y = x + 2. As x approaches infinity or negative infinity, the term 1/x approaches zero, leaving the linear function x + 2 as the oblique asymptote.
4. Using Limits to Confirm Asymptotes
Limits can be used to confirm the presence and equations of asymptotes. For horizontal and oblique asymptotes, one evaluates the limit of the function as x approaches infinity or negative infinity. If the limit exists and equals a constant (for horizontal asymptotes) or a linear function (for oblique asymptotes), that constant or linear function is the equation of the asymptote. For vertical asymptotes, limits are used to confirm the behavior of the function as it approaches the vertical asymptote, often resulting in positive or negative infinity, indicating the function’s approach towards the vertical line.
5. Graphical Analysis for Asymptotes
Graphical analysis provides a visual method for identifying asymptotes. By plotting the graph of a function, one can observe the behavior of the function as it approaches certain lines. Vertical asymptotes are identified by the function’s approach towards a vertical line without touching it, often with the graph increasing or decreasing without bound on either side of the line. Horizontal and oblique asymptotes are seen as the function’s approach towards a horizontal or slanted line, respectively, as x increases or decreases without bound. While graphical analysis can provide insights, it’s crucial to use algebraic methods to precisely determine the equations of asymptotes.
What is the primary method for identifying vertical asymptotes in rational functions?
+The primary method involves setting the denominator equal to zero and solving for x, as vertical asymptotes occur where the function is undefined due to division by zero.
How do you determine if a rational function has a horizontal asymptote?
+A rational function has a horizontal asymptote if the degree of the numerator is less than or equal to the degree of the denominator. The equation of the horizontal asymptote depends on whether the degrees are equal (ratio of leading coefficients) or the numerator's degree is less (y = 0).
What is the role of limits in confirming asymptotes?
+Limits are used to confirm the presence and equations of asymptotes by evaluating the behavior of the function as x approaches infinity, negative infinity, or a specific value. They help in mathematically validating the visual observations from graphical analysis.
In conclusion, finding asymptotes is a critical aspect of understanding the behavior of functions, particularly in the context of calculus and algebra. Through the five methods outlined—identifying vertical asymptotes, determining horizontal asymptotes, discovering oblique asymptotes, using limits, and graphical analysis—one can comprehensively analyze functions to identify and understand their asymptotic behavior. Each method contributes uniquely to the overall understanding, highlighting the importance of a multifaceted approach to asymptote identification and analysis.