Calculating half of a number is a fundamental mathematical operation that can be applied in various real-life situations, from dividing a pizza among friends to determining the midpoint of a numerical range. While the concept of finding half of a number seems straightforward, there are multiple methods to achieve this, each with its own utility depending on the context. In this article, we'll explore five different ways to calculate half of a number, ranging from basic arithmetic to more advanced mathematical concepts.
Key Points
- Basic division method for calculating half
- Multiplication by 0.5 as an alternative approach
- Utilizing fractions to find half of a number
- Geometric approach for visual learners
- Algebraic method for more complex scenarios
Basic Division Method

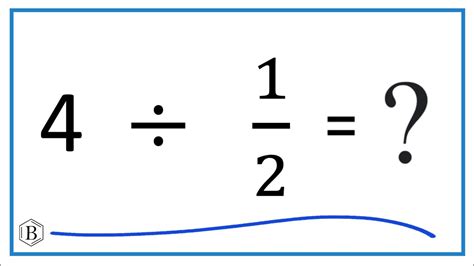
The most direct way to find half of a number is by dividing it by 2. This method is straightforward and can be applied universally, whether you’re dealing with integers, decimals, or fractions. For example, to find half of 10, you would simply divide 10 by 2, resulting in 5. This method can be expressed as: Number / 2 = Half. The simplicity of this approach makes it accessible and easy to understand, even for those with limited mathematical background.
Multiplication by 0.5
An alternative and equally effective method for calculating half of a number is by multiplying it by 0.5. This approach works because 0.5 is equivalent to 1⁄2. Therefore, multiplying any number by 0.5 will yield its half. For instance, to find half of 20 using this method, you would multiply 20 by 0.5, giving you 10. This can be represented as: Number * 0.5 = Half. The multiplication method can be particularly useful when dealing with decimals or in situations where division by 2 might not be as straightforward.
| Method | Formula | Example |
|---|---|---|
| Division | Number / 2 | 10 / 2 = 5 |
| Multiplication by 0.5 | Number * 0.5 | 10 * 0.5 = 5 |
Utilizing Fractions

Fractions provide another means to calculate half of a number. By multiplying the number by 1⁄2, you effectively find its half. This method is especially intuitive when dealing with fractions themselves, as it maintains the fractional form. For example, to find half of 3⁄4, you would multiply 3⁄4 by 1⁄2, resulting in 3⁄8. The fractional method can be expressed as: Number * 1⁄2 = Half. It’s a versatile approach that can be applied across different types of numbers and is particularly useful in mathematical problems involving ratios and proportions.
Geometric Approach
For those who prefer visual learning, a geometric approach can be an engaging way to understand the concept of halves. By dividing a shape, such as a rectangle or a circle, into two equal parts, you can visually represent what it means to find half of something. This method is especially useful in geometry and design, where understanding proportions and divisions of shapes is crucial. For example, if you have a rectangle that is 10 units long and you want to find the midpoint, you would divide the length by 2, getting 5 units. This geometric approach can help in understanding spatial relationships and proportions.
Algebraic Method
In more advanced mathematical contexts, such as algebra, finding half of a variable or an expression can be approached through the multiplication of that variable or expression by 1⁄2. For instance, if you want to find half of x, you would write it as (1⁄2)x or 0.5x. This method is essential in solving equations and manipulating expressions to isolate variables. The algebraic approach to finding halves is represented as: (1⁄2) * Expression = Half of Expression. It demonstrates the flexibility and applicability of mathematical operations across different branches of mathematics.
Forward-Looking Implications
The ability to calculate halves of numbers has numerous implications beyond basic arithmetic. It forms the foundation for understanding more complex mathematical concepts, such as ratios, proportions, and percentages. In real-world applications, from cooking and finance to science and engineering, being able to find halves (or any fractional part) of quantities is indispensable. The versatility of the methods outlined—division, multiplication by 0.5, using fractions, geometric approach, and algebraic method—ensures that individuals can adapt their calculation strategy based on the context and the type of problem they are solving.
What is the most straightforward way to calculate half of a number?
+The most straightforward way to calculate half of a number is by dividing it by 2 or multiplying it by 0.5.
How do fractions help in calculating halves?
+Fractions help by allowing you to multiply the number by 1/2, providing a direct way to find its half, especially useful when dealing with ratios and proportions.
What are the practical applications of finding halves in real life?
+Practical applications include cooking, finance, science, and engineering, where understanding and calculating proportions and parts of quantities are essential.
In conclusion, calculating halves of numbers is a fundamental skill with broad applications across various fields. The five methods discussed—division, multiplication by 0.5, fractions, geometric approach, and algebraic method—demonstrate the richness and versatility of mathematical operations. Whether you’re dealing with simple arithmetic or complex algebraic expressions, understanding how to find halves is crucial for problem-solving and critical thinking in mathematics and beyond.