The Gauss-Jordan method is a powerful tool for solving systems of linear equations, and its applications extend far beyond the realm of mathematics into various fields such as physics, engineering, and computer science. This method, an extension of Gaussian elimination, allows for the transformation of a matrix into reduced row echelon form (RREF), making it easier to solve for the variables in a system of equations. In this article, we will explore five significant ways the Gauss-Jordan method is utilized, demonstrating its versatility and importance in problem-solving.
Key Points
- The Gauss-Jordan method is used for solving systems of linear equations by transforming the augmented matrix into reduced row echelon form.
- It has applications in linear algebra, including finding the inverse of a matrix and determining the rank of a matrix.
- The method is crucial in physics and engineering for solving problems related to electrical circuits, structural analysis, and dynamic systems.
- In computer science, the Gauss-Jordan method is applied in areas such as computer graphics and machine learning for tasks like data transformation and feature selection.
- The method also finds use in cryptography for encrypting and decrypting messages, highlighting its role in information security.
Application in Linear Algebra

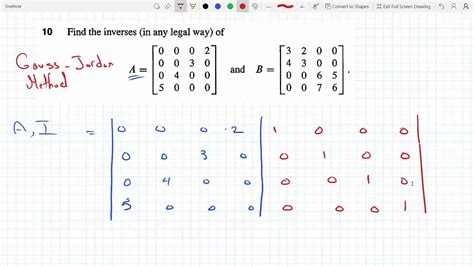
The Gauss-Jordan method is foundational in linear algebra, particularly for solving systems of linear equations, finding the inverse of a matrix, and determining the rank of a matrix. By transforming the augmented matrix of a system into reduced row echelon form, one can easily identify the solutions to the system. This process involves a series of row operations—swapping rows, multiplying a row by a non-zero scalar, and adding a multiple of one row to another—aimed at creating a matrix where the leading entry in each row is to the right of the leading entry in the row above it, and all entries below and above a leading entry are zero.
Matrix Inversion and Rank Determination
For matrix inversion, the Gauss-Jordan method involves augmenting the matrix with the identity matrix of the same size and then performing row operations to transform the original matrix into the identity matrix. If successful, the resulting matrix on the right side of the augmentation bar is the inverse of the original matrix. This process also helps in determining the rank of a matrix, which is the maximum number of linearly independent rows (or columns) in the matrix. The rank can be identified by counting the number of leading entries (pivots) in the reduced row echelon form of the matrix.
| Application | Description |
|---|---|
| Matrix Inversion | Transforming a matrix into the identity matrix to find its inverse. |
| Rank Determination | Counting the number of leading entries in the reduced row echelon form to find the rank. |
Physics and Engineering Applications

In physics and engineering, the Gauss-Jordan method is pivotal for solving problems related to electrical circuits, structural analysis, and dynamic systems. For electrical circuits, it helps in finding currents and voltages by solving the system of equations derived from Kirchhoff’s laws. In structural analysis, the method is used to determine stresses and strains in beams and other structures, solving the system of linear equations that represents the equilibrium conditions of the structure. For dynamic systems, the Gauss-Jordan method aids in solving the equations of motion, which are often linear differential equations that can be represented as systems of linear algebraic equations in the frequency domain.
Real-World Examples
A practical example in electrical engineering involves a circuit with multiple loops and branches, where applying the Gauss-Jordan method to the system of equations derived from the circuit analysis yields the currents in each branch. Similarly, in civil engineering, the method can be applied to find the forces and moments acting on the members of a truss, ensuring that the structure can withstand external loads without failure.
How does the Gauss-Jordan method help in electrical circuit analysis?
+The Gauss-Jordan method helps in electrical circuit analysis by solving the system of equations derived from Kirchhoff's laws, allowing for the determination of currents and voltages in the circuit.
What role does the Gauss-Jordan method play in structural analysis?
+In structural analysis, the Gauss-Jordan method is used to solve the system of linear equations that represents the equilibrium conditions of the structure, helping to determine stresses and strains.
Computer Science Applications
In computer science, the Gauss-Jordan method finds applications in areas such as computer graphics and machine learning. In computer graphics, it is used for tasks like data transformation and projection, where linear transformations are represented by matrices and need to be inverted or solved for specific parameters. In machine learning, the method can be applied in feature selection and data preprocessing, where solving systems of linear equations can help in identifying relevant features or transforming data into a more suitable format for analysis.
Machine Learning and Data Analysis
In machine learning, the Gauss-Jordan method can be used to solve systems of linear equations that arise from linear regression models, helping to find the coefficients of the regression line. Additionally, in data analysis, the method can aid in solving systems of equations that represent constraints or relationships between different variables, facilitating data transformation and feature extraction.
In conclusion, the Gauss-Jordan method is a versatile and powerful tool with far-reaching applications across various disciplines. Its ability to solve systems of linear equations, invert matrices, and determine ranks makes it an indispensable technique in linear algebra, physics, engineering, computer science, and beyond. As computational methods continue to evolve, the fundamental principles of the Gauss-Jordan method will remain a cornerstone of problem-solving in these fields.