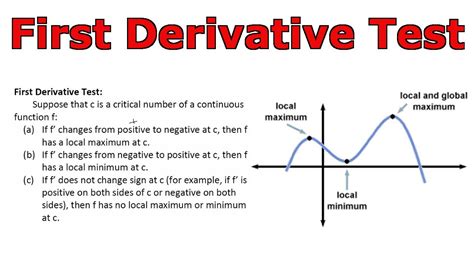
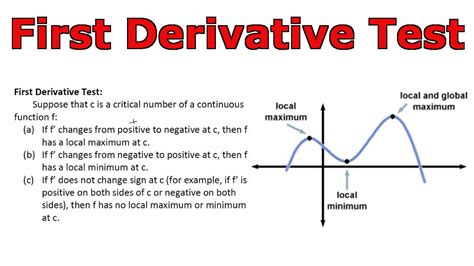
The first derivative test is a fundamental concept in calculus, used to determine the nature of critical points in a function. It is a crucial tool for analyzing the behavior of functions and understanding their properties. In this article, we will delve into the world of the first derivative test, exploring its definition, application, and significance in mathematics.
To begin with, let’s establish the foundation of the first derivative test. The concept revolves around the idea of identifying critical points in a function, which are points where the derivative of the function is zero or undefined. These points are crucial because they can indicate the presence of local maxima or minima, as well as points of inflection. The first derivative test provides a systematic approach to classifying these critical points, allowing us to determine whether they correspond to a local maximum, minimum, or neither.
Definition and Application

The first derivative test is defined as follows: given a function f(x) and a critical point c, if the derivative f’(x) changes sign from positive to negative as x increases through c, then c is a local maximum. Conversely, if the derivative changes sign from negative to positive as x increases through c, then c is a local minimum. If the derivative does not change sign, then c is neither a local maximum nor a local minimum.
To apply the first derivative test, we need to follow a series of steps:
- Find the critical points of the function by solving for the values of x that make the derivative equal to zero or undefined.
- Evaluate the derivative at points to the left and right of each critical point.
- Determine the sign of the derivative at these points.
- Use the sign changes to classify the critical points as local maxima, minima, or neither.
Key Points
- The first derivative test is used to classify critical points in a function.
- Critical points are points where the derivative is zero or undefined.
- The test involves evaluating the derivative at points to the left and right of each critical point.
- Sign changes in the derivative indicate the presence of local maxima or minima.
- The test is a fundamental tool for analyzing the behavior of functions.
Example Applications
To illustrate the application of the first derivative test, let’s consider a few examples. Suppose we have a function f(x) = x^3 - 6x^2 + 9x + 2. To find the critical points, we take the derivative and set it equal to zero:
f’(x) = 3x^2 - 12x + 9 = 0
Solving for x, we find that the critical points are x = 1 and x = 3. To classify these points, we evaluate the derivative at points to the left and right of each critical point:
| x | f’(x) |
|---|---|
| 0 | 9 |
| 1 | 0 |
| 2 | -3 |
| 3 | 0 |
| 4 | 9 |
From the table, we can see that the derivative changes sign from positive to negative as x increases through x = 1, indicating that x = 1 is a local maximum. Similarly, the derivative changes sign from negative to positive as x increases through x = 3, indicating that x = 3 is a local minimum.
Technical Specifications
The first derivative test has several technical specifications that are essential to its application. These include:
- Continuity: The function must be continuous at the critical point.
- Differentiability: The function must be differentiable at points to the left and right of the critical point.
- Sign changes: The derivative must change sign as x increases through the critical point.
Forward-Looking Implications

The first derivative test has significant implications for the study of calculus and its applications. By providing a systematic approach to classifying critical points, the test enables us to:
- Optimize functions: By identifying local maxima and minima, we can optimize functions to achieve desired outcomes.
- Analyze behavior: The test helps us understand the behavior of functions, including their increasing and decreasing intervals.
- Model real-world phenomena: The first derivative test is essential for modeling real-world phenomena, such as population growth, economic trends, and physical systems.
In conclusion, the first derivative test is a fundamental concept in calculus that provides a systematic approach to classifying critical points in a function. By understanding the definition, application, and technical specifications of the test, we can analyze the behavior of functions and optimize them to achieve desired outcomes.
What is the purpose of the first derivative test?
+The first derivative test is used to classify critical points in a function, determining whether they correspond to a local maximum, minimum, or neither.
How do I apply the first derivative test?
+To apply the first derivative test, find the critical points of the function, evaluate the derivative at points to the left and right of each critical point, and determine the sign of the derivative at these points.
What are the technical specifications of the first derivative test?
+The technical specifications of the first derivative test include continuity, differentiability, and sign changes in the derivative.