Calculating the area of various shapes and surfaces is a fundamental concept in geometry and mathematics, with applications spanning architecture, engineering, and design. The approach to finding the area depends on the shape in question, as different formulas and techniques are applied to different geometric figures. Here, we will explore five common methods for calculating area, each tailored to specific types of shapes or scenarios.
Key Points
- Understanding the formula for the area of a rectangle and its application
- Calculating the area of a triangle using base and height
- Applying the formula for the area of a circle with precision
- Using the Shoelace formula for the area of a polygon
- Understanding how to calculate the area of a trapezoid
Calculating the Area of a Rectangle
The area of a rectangle is one of the most straightforward calculations in geometry. It is found by multiplying the length of the rectangle by its width. The formula for this is Area = length × width. For example, if a rectangle has a length of 10 cm and a width of 5 cm, its area would be 10 cm × 5 cm = 50 square cm. This formula is widely used in construction, furniture design, and any field where the size of rectangular surfaces needs to be quantified.
Understanding the Formula
The simplicity of the rectangle’s area formula makes it a foundational element in more complex calculations. It’s essential to remember that the units of measurement for length and width must be the same to ensure the area is calculated in the correct square units. This formula also applies to squares, where all sides are of equal length, making the calculation even more straightforward.
Calculating the Area of a Triangle
The area of a triangle can be calculated using the formula Area = ½ × base × height. Here, the base refers to any side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex. This formula is versatile and can be applied to all types of triangles, whether they are right-angled, isosceles, or scalene. For instance, a triangle with a base of 8 cm and a height of 6 cm would have an area of ½ × 8 cm × 6 cm = 24 square cm.
Application in Real-World Scenarios
The area of a triangle is crucial in various real-world applications, including architecture, where the size and shape of triangular elements in structures need to be precisely calculated for stability and design purposes. It’s also vital in surveying, where the areas of triangular plots of land are calculated for legal and developmental purposes.
Calculating the Area of a Circle
The area of a circle is given by the formula Area = π × radius^2, where π (pi) is a constant approximately equal to 3.14159. This formula requires knowing the radius of the circle, which is the distance from the center of the circle to any point on its circumference. For example, a circle with a radius of 4 cm would have an area of π × (4 cm)^2 = approximately 50.265 square cm. This calculation is essential in designing circular structures, pipes, and any component that involves circular surfaces.
Practical Applications
The formula for the area of a circle has numerous practical applications, including the design of circular buildings, the calculation of the area of circular fields for agricultural purposes, and in engineering, where the cross-sectional area of pipes and tubes is critical for determining flow rates and capacities.
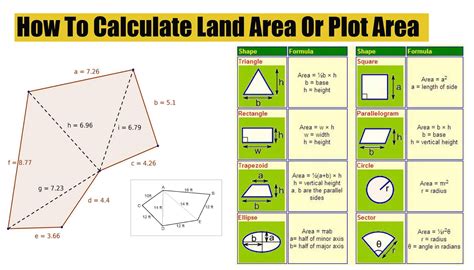
Using the Shoelace Formula for Polygons
The Shoelace formula is a mathematical algorithm used to determine the area of a simple polygon whose vertices are given by their coordinates in the plane. The formula is given by Area = ½ |(x1y2 + x2y3 + … + xn-1yn + xn y1) - (y1x2 + y2x3 + … + yn-1xn + yn x1)|, where (x1, y1), (x2, y2), …, (xn, yn) are the coordinates of the vertices of the polygon. This formula is particularly useful in geography and computer graphics, where the areas of complex shapes need to be calculated with precision.
Complexity and Application
The Shoelace formula, while more complex than the formulas for basic shapes, provides a powerful tool for calculating the area of any polygon, given its vertices. This is especially useful in Geographic Information Systems (GIS), where the areas of irregularly shaped territories, water bodies, or forest areas need to be accurately measured for planning, conservation, and management purposes.
Calculating the Area of a Trapezoid
A trapezoid is a quadrilateral with at least one pair of parallel sides, and its area can be calculated using the formula Area = ½ × (sum of parallel sides) × height. The height is the perpendicular distance between the parallel sides. For example, a trapezoid with parallel sides of 10 cm and 15 cm, and a height of 6 cm, would have an area of ½ × (10 cm + 15 cm) × 6 cm = 75 square cm. This formula is essential in construction, where trapezoidal shapes are common in the design of buildings, bridges, and other structures.
Importance in Construction
The calculation of a trapezoid’s area is vital in various aspects of construction and engineering. It helps in estimating the amount of material needed for roofing, the design of trapezoidal cross-sections in bridges for optimal strength, and in calculating the area of trapezoidal plots of land for development purposes.
| Shape | Formula | Example |
|---|---|---|
| Rectangle | length × width | 10 cm × 5 cm = 50 square cm |
| Triangle | ½ × base × height | ½ × 8 cm × 6 cm = 24 square cm |
| Circle | π × radius^2 | π × (4 cm)^2 = approximately 50.265 square cm |
| Polygon | Shoelace formula | Depends on the coordinates of the vertices |
| Trapezoid | ½ × (sum of parallel sides) × height | ½ × (10 cm + 15 cm) × 6 cm = 75 square cm |
What is the most common mistake when calculating the area of a circle?
+Forgetting to square the radius when applying the formula Area = π × radius^2 is a common mistake. It’s crucial to ensure all calculations are performed correctly to obtain the accurate area.
How does the Shoelace formula handle polygons with a large number of sides?
+The Shoelace formula is versatile and can handle polygons with any number of sides, provided the coordinates of all vertices are known. However, the complexity of the calculation increases with the number of sides, making computational tools essential for large polygons.
What are the practical applications of calculating the area of a trapezoid?
+Calculating the area of a trapezoid has practical applications in construction, engineering, and architecture, particularly in designing roofs, bridges, and structures with trapezoidal cross-sections, and in estimating material requirements.