Even and odd functions are fundamental concepts in mathematics, particularly in algebra and calculus. These functions have unique properties that make them essential in various mathematical operations and real-world applications. In this article, we will delve into the world of even and odd functions, exploring their definitions, properties, and practical uses. We will also examine five key ways in which even and odd functions work, providing a comprehensive understanding of these mathematical building blocks.
Key Points
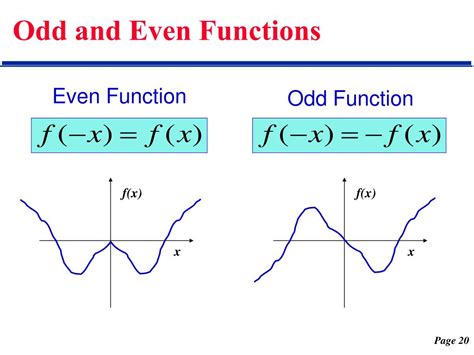
- Even functions satisfy the condition f(x) = f(-x) for all x in the domain.
- Odd functions satisfy the condition f(-x) = -f(x) for all x in the domain.
- Even and odd functions have distinct symmetry properties.
- These functions are used in various mathematical operations, such as integration and differentiation.
- Real-world applications of even and odd functions include signal processing, physics, and engineering.
Definition and Properties of Even and Odd Functions

Even functions are defined as functions that satisfy the condition f(x) = f(-x) for all x in the domain. This means that if we replace x with -x, the function remains unchanged. On the other hand, odd functions satisfy the condition f(-x) = -f(x) for all x in the domain. This implies that if we replace x with -x, the function changes sign. These definitions have significant implications for the properties and behavior of even and odd functions.
Symmetry Properties of Even and Odd Functions
Even functions have symmetry about the y-axis, meaning that if we reflect the graph of the function about the y-axis, the resulting graph is identical to the original. In contrast, odd functions have rotational symmetry about the origin, meaning that if we rotate the graph of the function by 180 degrees about the origin, the resulting graph is identical to the original. These symmetry properties are essential in understanding the behavior of even and odd functions.
| Function Type | Definition | Symmetry |
|---|---|---|
| Even Function | f(x) = f(-x) | Symmetry about the y-axis |
| Odd Function | f(-x) = -f(x) | Rotational symmetry about the origin |
5 Ways Even and Odd Functions Work
Now that we have explored the definitions and properties of even and odd functions, let’s examine five key ways in which they work.
1. Integration and Differentiation
Even and odd functions have distinct properties when it comes to integration and differentiation. The integral of an even function is even, while the integral of an odd function is odd. Similarly, the derivative of an even function is odd, while the derivative of an odd function is even. These properties are essential in various mathematical operations, such as finding the area under curves and solving differential equations.
2. Signal Processing
Even and odd functions are used extensively in signal processing, particularly in filtering and modulation techniques. Even functions are used to represent symmetric signals, while odd functions are used to represent antisymmetric signals. Understanding the properties of even and odd functions is crucial in designing and analyzing signal processing systems.
3. Physics and Engineering
Even and odd functions have numerous applications in physics and engineering, particularly in the study of waves and vibrations. Even functions are used to represent standing waves, while odd functions are used to represent traveling waves. These functions are also used in the analysis of electrical circuits, mechanical systems, and other physical phenomena.
4. Mathematical Modeling
Even and odd functions are used in mathematical modeling to represent real-world phenomena, such as population growth, chemical reactions, and financial markets. These functions are essential in developing and analyzing mathematical models, allowing us to make predictions and understand complex systems.
5. Computer Science and Data Analysis
Even and odd functions have applications in computer science and data analysis, particularly in machine learning and data visualization. These functions are used to represent and analyze complex data sets, allowing us to identify patterns and trends. Understanding the properties of even and odd functions is crucial in developing and applying machine learning algorithms and data visualization techniques.
What is the difference between an even function and an odd function?
+An even function satisfies the condition f(x) = f(-x) for all x in the domain, while an odd function satisfies the condition f(-x) = -f(x) for all x in the domain.
What are some real-world applications of even and odd functions?
+Even and odd functions have applications in signal processing, physics, engineering, mathematical modeling, computer science, and data analysis.
How do even and odd functions relate to symmetry?
+Even functions have symmetry about the y-axis, while odd functions have rotational symmetry about the origin.
In conclusion, even and odd functions are fundamental concepts in mathematics, with distinct properties and applications. Understanding these functions is crucial for working with mathematical models, signal processing, physics, engineering, and computer science. By examining the definitions, properties, and applications of even and odd functions, we can gain a deeper appreciation for the importance of these mathematical building blocks in various fields.



