Understanding the end behavior of a function is crucial in mathematics, particularly in algebra and calculus. It helps in analyzing how the function behaves as the input (or x) gets arbitrarily large or small. In this comprehensive guide, we will delve into the concept of end behavior charts, their importance, and how to analyze them for different types of functions, including polynomial, rational, and exponential functions.
Introduction to End Behavior Charts
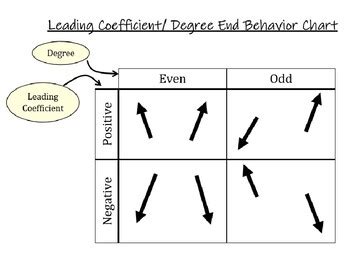
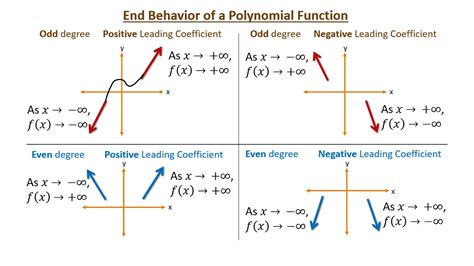
End behavior charts are graphical representations that show how a function behaves as x approaches positive or negative infinity. These charts are invaluable tools for understanding the long-run behavior of functions, which is essential in various mathematical and real-world applications. By analyzing end behavior charts, one can predict the function’s behavior, identify limits, and understand the function’s overall shape and characteristics.
Key Points
- End behavior charts illustrate how a function behaves as x approaches infinity or negative infinity.
- Understanding end behavior is crucial for analyzing limits and the overall shape of a function.
- Polynomial, rational, and exponential functions have distinct end behaviors based on their degrees and leading coefficients.
- End behavior analysis is essential in calculus for understanding function limits and continuity.
- Real-world applications of end behavior include modeling population growth, economic trends, and physical phenomena.
Polynomial Functions and End Behavior
Polynomial functions are among the simplest to analyze for end behavior. The end behavior of a polynomial function is determined by its degree and the leading coefficient. For a polynomial of degree n, if the leading coefficient is positive, the function rises on the right (as x approaches infinity) and falls on the left (as x approaches negative infinity) if n is even, or it rises on both ends if n is odd. Conversely, if the leading coefficient is negative, the function falls on the right and rises on the left for even degrees, or falls on both ends for odd degrees.
| Polynomial Degree | Leading Coefficient | End Behavior |
|---|---|---|
| Even (n) | Positive | Rises on both ends |
| Even (n) | Negative | Falls on both ends |
| Odd (n) | Positive | Rises on the right, falls on the left |
| Odd (n) | Negative | Falls on the right, rises on the left |

Rational Functions and End Behavior
Rational functions, which are ratios of polynomial functions, have end behaviors that depend on the degrees of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the function approaches zero as x approaches infinity or negative infinity. If the degrees are equal, the function approaches the ratio of the leading coefficients. If the degree of the numerator is greater, the function behaves like a polynomial of the difference in degrees, with the leading coefficient of the numerator determining the direction.
Exponential Functions and End Behavior

Exponential functions have a distinct end behavior that is determined by their base. If the base is greater than 1, the function rises exponentially as x approaches infinity and approaches zero as x approaches negative infinity. If the base is between 0 and 1, the function behaves oppositely, falling as x approaches infinity and rising as x approaches negative infinity. For bases less than 0, the function’s end behavior alternates due to the properties of negative exponents.
Real-World Applications of End Behavior Analysis
Understanding the end behavior of functions is not just theoretically important but also has numerous practical applications. In economics, it helps in modeling long-term trends and predicting economic growth or decline. In biology, end behavior analysis is crucial for understanding population dynamics and the spread of diseases. In physics and engineering, it is used to model the behavior of complex systems over time, such as the trajectory of projectiles or the growth of electrical currents.
What determines the end behavior of a polynomial function?
+The end behavior of a polynomial function is determined by its degree and the leading coefficient. The degree tells us if the function rises or falls, and the leading coefficient tells us the direction of the rise or fall.
How does the end behavior of a rational function differ from that of a polynomial function?
+The end behavior of a rational function depends on the comparison of the degrees of the numerator and denominator. It can approach a horizontal asymptote, behave like a polynomial, or approach zero, depending on the degree comparison.
What is the significance of end behavior in real-world applications?
+End behavior is crucial for predicting long-term trends, understanding system behaviors over time, and making informed decisions in fields like economics, biology, physics, and engineering.
In conclusion, understanding end behavior charts is fundamental for analyzing functions in mathematics and applying these concepts to real-world problems. By recognizing the patterns and rules that govern the end behavior of different types of functions, individuals can better comprehend complex phenomena and make more accurate predictions about future trends and behaviors.