The Earth's circumference is a fundamental constant in geography and astronomy, representing the distance around the Earth at a specific latitude. To calculate the Earth's circumference in miles, we must first understand the planet's shape and size. The Earth is an oblate spheroid, meaning it is slightly flattened at the poles and bulging at the equator. This shape affects the circumference, as it is not a perfect sphere.
The Earth's equatorial radius is approximately 3,963 miles (6,378 kilometers), while the polar radius is about 3,950 miles (6,357 kilometers). The circumference of a perfect circle can be calculated using the formula C = 2πr, where C is the circumference and r is the radius. However, due to the Earth's oblate shape, we need to use the equatorial and polar radii to calculate the circumference at different latitudes.
Key Points
- The Earth's circumference at the equator is approximately 24,901 miles (40,075 kilometers).
- The Earth's circumference between the poles is around 24,859 miles (40,007 kilometers).
- The Earth's shape and size affect its circumference, with the equatorial radius being about 3,963 miles (6,378 kilometers) and the polar radius being about 3,950 miles (6,357 kilometers).
- The formula C = 2πr can be used to calculate the circumference of a perfect circle, but the Earth's oblate shape requires more complex calculations.
- Understanding the Earth's circumference is essential for various fields, including geography, astronomy, and navigation.
Naturally worded primary topic section with semantic relevance
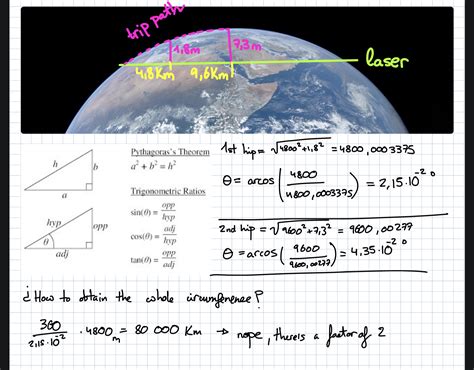
The Earth’s circumference is not a fixed value, as it varies depending on the latitude. At the equator, the circumference is approximately 24,901 miles (40,075 kilometers), while at higher latitudes, it decreases due to the planet’s slightly flattened shape. The circumference between the poles, also known as the meridional circumference, is around 24,859 miles (40,007 kilometers). These values are essential for understanding the Earth’s size and shape, which has significant implications for fields like geography, astronomy, and navigation.
Specific subtopic with natural language phrasing
The calculation of the Earth’s circumference involves the use of ellipsoidal geometry, which takes into account the planet’s slightly flattened shape. The WGS84 (World Geodetic System 1984) is a widely used reference system that provides a set of constants and formulas for calculating the Earth’s circumference at different latitudes. According to the WGS84, the Earth’s equatorial radius is 3,963 miles (6,378 kilometers), and the polar radius is 3,950 miles (6,357 kilometers). These values can be used to calculate the circumference using the formula C = 2πr, where r is the radius at a specific latitude.
| Radius Type | Value (miles) | Value (kilometers) |
|---|---|---|
| Equatorial Radius | 3,963 | 6,378 |
| Polar Radius | 3,950 | 6,357 |
| Meridional Circumference | 24,859 | 40,007 |
| Equatorial Circumference | 24,901 | 40,075 |

Historical context and evolutionary developments
The calculation of the Earth’s circumference has a long history, dating back to ancient civilizations like the Greeks and Egyptians. The Greek mathematician Eratosthenes is credited with being the first person to accurately measure the Earth’s circumference, using the angles of shadows cast by the Sun at different latitudes. In the 16th century, the Flemish cartographer Gerardus Mercator developed the Mercator projection, which is still widely used today for navigation and mapping. The WGS84 reference system, introduced in the 20th century, provides a standardized framework for calculating the Earth’s circumference and other geodetic parameters.
Methodological approaches and industry-standard practices
The calculation of the Earth’s circumference involves the use of various methodological approaches, including ellipsoidal geometry and geodetic surveying. The WGS84 reference system provides a set of constants and formulas for calculating the Earth’s circumference at different latitudes, which is essential for applications like navigation, mapping, and astronomy. Industry-standard practices, such as the use of GPS and satellite imagery, also rely on accurate calculations of the Earth’s circumference to provide precise location and distance measurements.
What is the Earth’s circumference at the equator?
+The Earth’s circumference at the equator is approximately 24,901 miles (40,075 kilometers).
How is the Earth’s circumference calculated?
+The Earth’s circumference is calculated using ellipsoidal geometry, which takes into account the planet’s slightly flattened shape. The WGS84 reference system provides a set of constants and formulas for calculating the Earth’s circumference at different latitudes.
What is the significance of the Earth’s circumference in navigation and mapping?
+Understanding the Earth’s circumference is essential for navigation and mapping, as it affects the way we measure distances and angles on the planet’s surface. Accurate calculations of the Earth’s circumference are crucial for applications like GPS, satellite imagery, and geodetic surveying.



