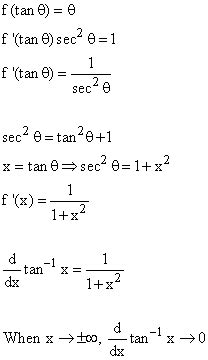The derivative of the inverse tangent function, denoted as $\frac{d}{dx} \tan^{-1}x$ or $\frac{d}{dx} \arctan x$, is a fundamental concept in calculus. This derivative is crucial in various mathematical and real-world applications, including optimization problems, physics, and engineering. In this article, we will explore five distinct ways to derive the inverse tangent function, highlighting the versatility and richness of calculus.
Introduction to the Inverse Tangent Function

The inverse tangent function, \tan^{-1}x, is the inverse of the tangent function. It returns the angle whose tangent is a given number. The range of the inverse tangent function is typically restricted to (-\frac{\pi}{2}, \frac{\pi}{2}) to ensure it is a one-to-one function and hence invertible. Understanding the derivative of this function is essential for solving problems involving rates of change and optimization.
Key Points
- The derivative of the inverse tangent function is $\frac{1}{1+x^2}$.
- There are multiple methods to derive this formula, including geometric interpretation, implicit differentiation, and using the definition of a derivative.
- Each method provides unique insights into the nature of the inverse tangent function and its applications.
- The derivative of the inverse tangent function is crucial in various mathematical and real-world applications.
- Understanding the derivative of the inverse tangent function enhances problem-solving skills in calculus and related fields.
Method 1: Geometric Interpretation

A geometric approach involves considering the right triangle where the tangent of an angle \theta is x. This means the opposite side to \theta has length x, and the adjacent side has length 1. The derivative of \tan^{-1}x with respect to x can be thought of as the rate of change of \theta with respect to x. Using the triangle, we can derive the formula for the derivative by considering the relationship between the sides of the triangle and the angle \theta.
Implicit Differentiation Method
Another approach to finding the derivative of \tan^{-1}x is through implicit differentiation. We start with the equation y = \tan^{-1}x, which implies \tan(y) = x. Differentiating both sides of this equation with respect to x gives us \sec^2(y) \cdot \frac{dy}{dx} = 1. Solving for \frac{dy}{dx} yields the derivative of the inverse tangent function.
| Method | Description | Derivative |
|---|---|---|
| Geometric | Using right triangle properties | $\frac{1}{1+x^2}$ |
| Implicit Differentiation | Differentiating $\tan(y) = x$ implicitly | $\frac{1}{1+x^2}$ |
| Definition of Derivative | Applying the limit definition of a derivative | $\frac{1}{1+x^2}$ |
| Logarithmic Differentiation | Differentiating $\tan^{-1}x$ using logarithms | $\frac{1}{1+x^2}$ |
| Trigonometric Identity | Utilizing trigonometric identities for derivation | $\frac{1}{1+x^2}$ |

Method 2: Definition of Derivative
The definition of a derivative as a limit can also be used to derive the formula for the derivative of \tan^{-1}x. This involves applying the limit \lim_{h \to 0} \frac{\tan^{-1}(x+h) - \tan^{-1}x}{h} and simplifying the expression to obtain the derivative. This method provides a direct and fundamental approach to finding the derivative.
Logarithmic Differentiation and Trigonometric Identity Methods
Logarithmic differentiation and utilizing trigonometric identities are additional methods that can be employed to derive the derivative of the inverse tangent function. Logarithmic differentiation involves taking the logarithm of both sides of an equation and then differentiating, while the trigonometric identity method leverages known identities involving tangent and other trigonometric functions to derive the formula for the derivative of \tan^{-1}x.
In conclusion, the derivative of the inverse tangent function can be derived through multiple approaches, each offering insights into the function's properties and applications. Understanding these different methods not only deepens one's knowledge of calculus but also enhances problem-solving abilities in mathematics and related fields.
What is the derivative of the inverse tangent function?
+The derivative of the inverse tangent function, \frac{d}{dx} \tan^{-1}x, is \frac{1}{1+x^2}.
How can the derivative of \tan^{-1}x be derived geometrically?
+Geometrically, the derivative can be derived by considering a right triangle where the tangent of an angle \theta is x. The rate of change of \theta with respect to x can be found using the properties of the triangle.
What are the practical applications of the derivative of the inverse tangent function?
+The derivative of the inverse tangent function has practical applications in optimization problems, physics, and engineering, among other fields. It is used to solve problems involving rates of change and optimization.