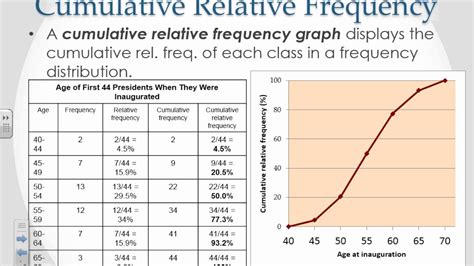
Cumulative frequency is a statistical concept that plays a crucial role in understanding and analyzing data distributions. It refers to the running total of frequencies, where each frequency is added to the previous one, providing a comprehensive view of how data accumulates over different categories or intervals. This concept is fundamental in various statistical analyses, including the creation of cumulative frequency distributions, which are essential for interpreting data trends, patterns, and outliers. In this article, we will delve into the concept of cumulative frequency, exploring its applications, benefits, and how it works in different contexts.
Understanding Cumulative Frequency

Cumulative frequency is calculated by adding the frequency of each category or interval to the sum of frequencies of all previous categories or intervals. This process creates a new set of frequencies that represent the cumulative total up to each point in the dataset. The concept is widely used in statistics, data analysis, and research to understand the distribution of data and to identify patterns or trends that might not be immediately apparent from the raw data. For instance, in a study examining the scores of students on a particular exam, cumulative frequency can help in understanding how many students scored below a certain threshold, which can be crucial for educational assessments and policy-making.
Applications of Cumulative Frequency
Cumulative frequency has numerous applications across various fields, including education, business, economics, and healthcare. In education, it can be used to analyze student performance and progression. In business, cumulative frequency can help in understanding customer behavior, sales trends, and market analysis. For example, a company might use cumulative frequency to analyze the sales of its products over time, identifying periods of high demand and adjusting production accordingly. In economics, it is used for macroeconomic analyses, such as understanding the distribution of income among the population. In healthcare, cumulative frequency can be applied to epidemiological studies, tracking the spread of diseases and the effectiveness of interventions.
| Field of Application | Use of Cumulative Frequency |
|---|---|
| Education | Analyzing student performance and progression |
| Business | Understanding customer behavior, sales trends, and market analysis |
| Economics | Macroeconomic analyses, including income distribution |
| Healthcare | Epidemiological studies and tracking disease spread |
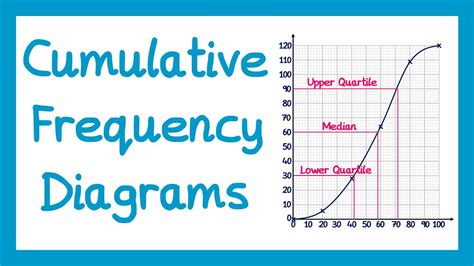
Calculating Cumulative Frequency

The process of calculating cumulative frequency involves several steps. First, the data must be organized into categories or intervals. Then, the frequency of each category or interval is determined. Finally, the cumulative frequency is calculated by adding the frequency of each category to the cumulative total of the previous categories. This process can be manual for small datasets but often requires the use of statistical software or spreadsheets for larger datasets due to the complexity and volume of data.
Interpreting Cumulative Frequency Distributions
Interpreting cumulative frequency distributions requires a good understanding of statistical concepts and the context of the data. Cumulative frequency distributions can be presented in the form of tables, graphs, or charts, with each format offering different insights into the data. For example, a cumulative frequency graph can show the proportion of data points that fall below a certain value, which is useful for identifying thresholds or cut-off points in the data. In quality control, this might be used to set standards for product defects, ensuring that a certain percentage of products meet the required specifications.
Key Points
- Cumulative frequency is a statistical concept used to understand data distributions.
- It has applications in education, business, economics, and healthcare.
- Cumulative frequency distributions can be used to analyze trends, patterns, and outliers in data.
- The calculation involves organizing data into categories, determining the frequency of each, and calculating the cumulative total.
- Interpreting cumulative frequency requires understanding statistical concepts and the data context.
Benefits and Limitations of Cumulative Frequency
The use of cumulative frequency offers several benefits, including the ability to identify trends and patterns in data, understand the distribution of data points, and make informed decisions based on statistical evidence. However, it also has limitations, such as the potential for misinterpretation if not properly understood and the requirement for a significant amount of data to be meaningful. Moreover, cumulative frequency alone may not provide a complete picture of the data, especially if the data contains outliers or if the categories are not appropriately defined.
Future Directions and Developments
As data analysis continues to evolve, the role of cumulative frequency is likely to expand, especially with the integration of advanced statistical techniques and machine learning algorithms. The ability to automate the calculation and interpretation of cumulative frequency distributions using software will make it more accessible and powerful for analysts. Furthermore, the application of cumulative frequency in emerging fields like data science and artificial intelligence could lead to new insights and methodologies for understanding complex data sets.
What is cumulative frequency, and why is it important?
+Cumulative frequency refers to the running total of frequencies, providing a comprehensive view of how data accumulates over different categories or intervals. It's important for understanding data distributions, identifying patterns and trends, and making informed decisions.
How is cumulative frequency calculated?
+Cumulative frequency is calculated by organizing data into categories, determining the frequency of each, and then adding each frequency to the cumulative total of the previous categories.
What are the applications of cumulative frequency in real-world scenarios?
+Cumulative frequency has applications in education, business, economics, and healthcare, among others, for analyzing trends, understanding distributions, and making data-driven decisions.
In conclusion, cumulative frequency is a powerful statistical tool that offers insights into data accumulation and distribution. Its applications are diverse, ranging from educational assessments to economic analyses. By understanding how to calculate and interpret cumulative frequency distributions, analysts can uncover patterns, trends, and outliers in data, ultimately informing decision-making processes across various sectors. As the field of data analysis continues to evolve, the importance of cumulative frequency in providing a foundational understanding of data distributions will remain a critical component of statistical inquiry.