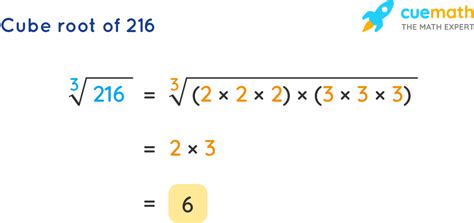The calculation of cube roots is a fundamental mathematical operation that has numerous applications in various fields, including engineering, physics, and mathematics. A cube root of a number is a value that, when multiplied by itself twice, gives the original number. For instance, the cube root of 27 is 3 because 3*3*3 = 27. In this article, we will delve into six distinct methods for calculating cube roots, each with its unique approach and application.
Key Points
- Understanding the concept of cube roots and their mathematical significance
- Exploring the prime factorization method for calculating cube roots
- Using long division to find cube roots of perfect cubes
- Applying the cube root formula for approximate calculations
- Utilizing calculators and computer software for efficient cube root calculations
- Employing numerical methods like the Babylonian method for iterative calculations
Understanding Cube Roots

Cube roots are the inverse operation of cubing a number. While cubing a number involves multiplying it by itself three times, finding the cube root of a number involves determining what value, when cubed, gives the original number. This operation is denoted by the symbol 3√ or the exponent 1⁄3. For example, 3√64 = 4, because 4*4*4 = 64.
Prime Factorization Method
The prime factorization method involves breaking down the given number into its prime factors and then identifying groups of three identical prime factors. Each group of three identical factors can be simplified to a single instance of that factor outside the cube root. For example, to find the cube root of 216, we factor 216 into its prime factors: 216 = 2*2*2*3*3*3. Grouping these into sets of three identical factors, we get (2*22)(3*3*3), which simplifies to 2*3 = 6. Therefore, 3√216 = 6.
| Number | Prime Factorization | Cube Root |
|---|---|---|
| 216 | 2*2*2*3*3*3 | 6 |
| 64 | 2*2*2*2*2*2 | 4 |
Long Division Method

The long division method for finding cube roots is somewhat similar to the long division method used for square roots. It involves a series of steps where the number is divided by a series of perfect cubes, and the remainders are used to find the cube root. This method is particularly useful for finding the cube roots of large numbers that are perfect cubes.
Using the Cube Root Formula
A more straightforward approach to finding cube roots, especially for numbers that are not perfect cubes, involves using a calculator or a numerical method. The cube root of a number x can be approximated using the formula 3√x ≈ x^(1⁄3), which can be calculated using a scientific calculator or a computer. For example, to find the cube root of 100, you would calculate 100^(1⁄3), which gives an approximate value.
Calculators and Computer Software
Most modern calculators and computer software packages, including spreadsheet programs like Microsoft Excel, have built-in functions for calculating cube roots. These tools provide a quick and accurate way to find cube roots, making them invaluable for both educational and professional applications. For instance, in Excel, you can use the formula “=A1^(1⁄3)” to calculate the cube root of a number in cell A1.
Numerical Methods - The Babylonian Method
The Babylonian method, also known as Heron’s method, is an iterative method used to find the cube root of a number. It starts with an initial guess and then repeatedly applies a formula to improve the guess until it converges to the actual cube root. The formula for the Babylonian method is x_{n+1} = (2x_n + N/x_n^2)/3, where x_n is the current guess, and N is the number for which we are finding the cube root. This method is efficient for finding cube roots of large numbers with high precision.
In conclusion, calculating cube roots is a fundamental mathematical operation that can be approached through various methods, each with its own advantages and applications. Whether using prime factorization, long division, the cube root formula, calculators, or numerical methods like the Babylonian method, understanding the concept and application of cube roots is essential in numerous fields. By selecting the appropriate method based on the context and the nature of the number, one can efficiently calculate cube roots to solve problems in mathematics, science, and engineering.
What is the cube root of a number?
+The cube root of a number is a value that, when multiplied by itself twice, gives the original number. It is denoted by the symbol 3√ or the exponent 1⁄3.
How do you calculate the cube root of a perfect cube using prime factorization?
+Break down the number into its prime factors, identify groups of three identical factors, and simplify each group to a single instance of that factor outside the cube root.
What is the Babylonian method for finding cube roots?
+The Babylonian method is an iterative method that starts with an initial guess and repeatedly applies the formula x_{n+1} = (2x_n + N/x_n^2)/3 to improve the guess until it converges to the actual cube root.