The Cos 2 Theta formula, also known as the double angle formula for cosine, is a fundamental concept in trigonometry that helps in simplifying complex expressions involving trigonometric functions. It states that cos(2θ) = cos^2(θ) - sin^2(θ), where θ is an angle in a right-angled triangle. This formula is crucial in various mathematical and real-world applications, including physics, engineering, and navigation.
Key Points
- The Cos 2 Theta formula is used to simplify expressions involving cosine and sine functions.
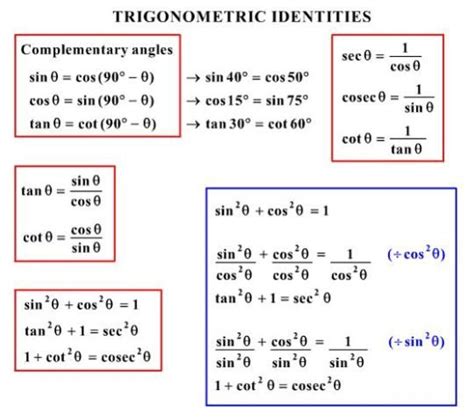
- It is derived from the Pythagorean identity, sin^2(θ) + cos^2(θ) = 1.
- The formula has numerous applications in physics, engineering, and navigation.
- It can be used to solve complex trigonometric equations and identities.
- The formula is a key concept in understanding the relationship between cosine and sine functions.
Naturally Worded Primary Topic Section with Semantic Relevance
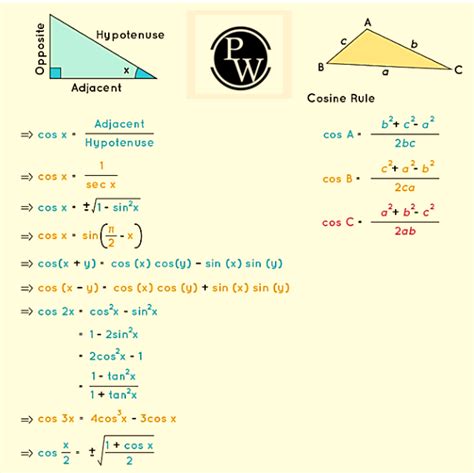
The Cos 2 Theta formula is often used in conjunction with other trigonometric identities to simplify complex expressions. For instance, the formula can be used to derive the double angle formula for sine, which states that sin(2θ) = 2sin(θ)cos(θ). This formula is essential in understanding the relationship between the sine and cosine functions and has numerous applications in physics and engineering.
Derivation of the Cos 2 Theta Formula
The Cos 2 Theta formula can be derived from the Pythagorean identity, sin^2(θ) + cos^2(θ) = 1. By rearranging this equation, we get cos^2(θ) = 1 - sin^2(θ). Substituting this expression into the formula cos(2θ) = cos^2(θ) - sin^2(θ), we get cos(2θ) = (1 - sin^2(θ)) - sin^2(θ) = 1 - 2sin^2(θ). This is a commonly used alternative form of the Cos 2 Theta formula.
| Trigonometric Identity | Formula |
|---|---|
| Pythagorean Identity | sin^2(θ) + cos^2(θ) = 1 |
| Cos 2 Theta Formula | cos(2θ) = cos^2(θ) - sin^2(θ) |
| Alternative Form | cos(2θ) = 1 - 2sin^2(θ) |
Applications of the Cos 2 Theta Formula
The Cos 2 Theta formula has numerous applications in physics, engineering, and navigation. For instance, it is used to calculate the displacement of objects in simple harmonic motion, where the displacement is given by the equation x(t) = Acos(ωt + φ). The formula is also used in electrical engineering to analyze the behavior of AC circuits, where the voltage and current are given by the equations V(t) = V0cos(ωt + φ) and I(t) = I0cos(ωt + φ), respectively.
Example Problems
To illustrate the application of the Cos 2 Theta formula, consider the following example problem: Find the value of cos(2θ) given that cos(θ) = 3⁄5 and sin(θ) = 4⁄5. Using the formula cos(2θ) = cos^2(θ) - sin^2(θ), we get cos(2θ) = (3⁄5)^2 - (4⁄5)^2 = 9⁄25 - 16⁄25 = -7⁄25.
What is the Cos 2 Theta formula?
+The Cos 2 Theta formula, also known as the double angle formula for cosine, states that cos(2θ) = cos^2(θ) - sin^2(θ), where θ is an angle in a right-angled triangle.
How is the Cos 2 Theta formula derived?
+The Cos 2 Theta formula can be derived from the Pythagorean identity, sin^2(θ) + cos^2(θ) = 1. By rearranging this equation, we get cos^2(θ) = 1 - sin^2(θ). Substituting this expression into the formula cos(2θ) = cos^2(θ) - sin^2(θ), we get cos(2θ) = (1 - sin^2(θ)) - sin^2(θ) = 1 - 2sin^2(θ).
What are the applications of the Cos 2 Theta formula?
+The Cos 2 Theta formula has numerous applications in physics, engineering, and navigation. It is used to calculate the displacement of objects in simple harmonic motion, analyze the behavior of AC circuits, and solve complex trigonometric equations and identities.
In conclusion, the Cos 2 Theta formula is a fundamental concept in trigonometry that helps in simplifying complex expressions involving trigonometric functions. Its derivation from the Pythagorean identity and its numerous applications in physics, engineering, and navigation make it a crucial tool for problem-solving and critical thinking. By understanding the Cos 2 Theta formula and its applications, individuals can develop a deeper appreciation for the underlying mathematics and improve their problem-solving skills.