Simple regression analysis is a statistical method used to model the relationship between a dependent variable and a single independent variable. The goal of simple regression is to create a linear equation that best predicts the value of the dependent variable based on the value of the independent variable. However, for the results of a simple regression analysis to be reliable and valid, certain assumptions must be met. In this article, we will explore the key assumptions of simple regression, their importance, and how to check if they are met.
Key Points
- Linearity assumption: The relationship between the independent and dependent variables should be linear.
- Independence assumption: Each observation should be independent of the others.
- Homoscedasticity assumption: The variance of the residuals should be constant across all levels of the independent variable.
- Normality assumption: The residuals should be normally distributed.
- No multicollinearity: The independent variable should not be highly correlated with itself.
Linearity Assumption

The linearity assumption states that the relationship between the independent and dependent variables should be linear. This means that the relationship between the variables can be represented by a straight line. If the relationship is not linear, the simple regression model may not accurately capture the relationship, and the results may be misleading. To check for linearity, a scatterplot of the data can be used. If the points on the scatterplot do not appear to follow a linear pattern, it may indicate a violation of the linearity assumption.
Checking for Linearity
There are several ways to check for linearity, including visual inspection of a scatterplot, using regression diagnostics such as the Ramsey RESET test, or transforming the data to achieve linearity. For example, if the relationship between the variables is curvilinear, a logarithmic or polynomial transformation may be used to achieve linearity.
| Assumption | Checking Method |
|---|---|
| Linearity | Scatterplot, Ramsey RESET test, transformation |
| Independence | Durbin-Watson test |
| Homoscedasticity | Breusch-Pagan test, White test |
| Normality | Shapiro-Wilk test, Q-Q plot |

Independence Assumption
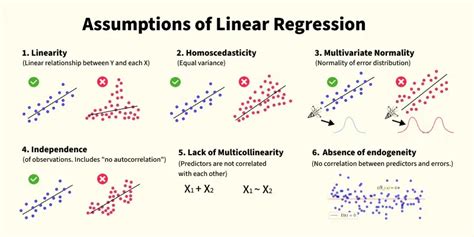
The independence assumption states that each observation should be independent of the others. This means that the observations should not be related to each other in any way. If the observations are not independent, it can lead to biased and inconsistent estimates of the regression coefficients. To check for independence, the Durbin-Watson test can be used. This test checks for autocorrelation in the residuals, which can indicate a violation of the independence assumption.
Dealing with Non-Independence
If the independence assumption is violated, there are several ways to address the issue. One approach is to use a different estimation method, such as generalized least squares (GLS), which can account for autocorrelation in the residuals. Another approach is to use a different model, such as a time series model, which is specifically designed to handle dependent data.
Homoscedasticity Assumption
The homoscedasticity assumption states that the variance of the residuals should be constant across all levels of the independent variable. This means that the spread of the residuals should be the same for all values of the independent variable. If the variance of the residuals is not constant, it can lead to biased and inconsistent estimates of the regression coefficients. To check for homoscedasticity, the Breusch-Pagan test or the White test can be used. These tests check for heteroscedasticity in the residuals, which can indicate a violation of the homoscedasticity assumption.
Dealing with Heteroscedasticity
If the homoscedasticity assumption is violated, there are several ways to address the issue. One approach is to use a different estimation method, such as weighted least squares (WLS), which can account for heteroscedasticity in the residuals. Another approach is to use a different model, such as a generalized linear model (GLM), which can handle non-constant variance in the residuals.
Normality Assumption
The normality assumption states that the residuals should be normally distributed. This means that the residuals should follow a normal distribution, with a mean of zero and a constant variance. If the residuals are not normally distributed, it can lead to biased and inconsistent estimates of the regression coefficients. To check for normality, the Shapiro-Wilk test or a Q-Q plot can be used. These tests check for normality in the residuals, which can indicate a violation of the normality assumption.
Dealing with Non-Normality
If the normality assumption is violated, there are several ways to address the issue. One approach is to use a different estimation method, such as the bootstrap method, which can account for non-normality in the residuals. Another approach is to use a different model, such as a non-parametric model, which does not require normality of the residuals.
What is the purpose of checking assumptions in simple regression?
+The purpose of checking assumptions in simple regression is to ensure that the results of the analysis are reliable and valid. If the assumptions are not met, the results may be biased and inconsistent, leading to incorrect conclusions.
How do I check for linearity in simple regression?
+To check for linearity in simple regression, you can use a scatterplot of the data, the Ramsey RESET test, or transformation of the data to achieve linearity.
What is the consequence of violating the independence assumption in simple regression?
+If the independence assumption is violated, it can lead to biased and inconsistent estimates of the regression coefficients, which can result in incorrect conclusions.
In conclusion, the assumptions of simple regression are essential to ensure that the results of the analysis are reliable and valid. By checking for linearity, independence, homoscedasticity, and normality, you can identify potential issues and take corrective action to address them. Remember that the assumptions of simple regression are not always met, and it’s essential to carefully interpret the results and consider alternative methods or models if necessary.



