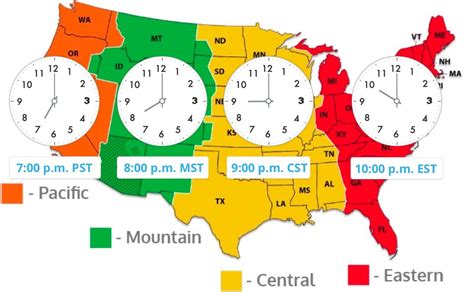
The antiderivative of the sine function, denoted as ∫sin(x) dx, is a fundamental concept in calculus that has numerous applications in various fields, including physics, engineering, and mathematics. The sine function, which is periodic with a period of 2π, is a continuous and differentiable function, making it an ideal candidate for integration.
To find the antiderivative of the sine function, we can use the fact that the derivative of the cosine function is equal to -sin(x). This relationship between the sine and cosine functions can be exploited to determine the antiderivative of sin(x). By applying the fundamental theorem of calculus, which states that differentiation and integration are inverse processes, we can deduce that the antiderivative of sin(x) is equal to -cos(x) + C, where C is the constant of integration.
Key Points
- The antiderivative of sin(x) is -cos(x) + C, where C is the constant of integration.
- The sine function is periodic with a period of 2π.
- The derivative of the cosine function is equal to -sin(x), which is used to determine the antiderivative of sin(x).
- The fundamental theorem of calculus states that differentiation and integration are inverse processes.
- The antiderivative of sin(x) has numerous applications in physics, engineering, and mathematics.
Derivation of the Antiderivative

The derivation of the antiderivative of sin(x) involves using the fact that the derivative of the cosine function is equal to -sin(x). This can be expressed mathematically as d(cos(x))/dx = -sin(x). By applying the fundamental theorem of calculus, we can rewrite this equation as ∫(-sin(x)) dx = cos(x) + C. Since the integral of -sin(x) is equal to the negative of the integral of sin(x), we can conclude that ∫sin(x) dx = -cos(x) + C.
Geometric Interpretation
The antiderivative of sin(x) can also be interpreted geometrically. The sine function represents the y-coordinate of a point on the unit circle, while the cosine function represents the x-coordinate. The antiderivative of sin(x) can be visualized as the area under the sine curve, which is equal to the negative of the area under the cosine curve. This geometric interpretation provides a useful tool for understanding the properties and behavior of the antiderivative of sin(x).
| Function | Derivative | Antiderivative |
|---|---|---|
| sin(x) | cos(x) | -cos(x) + C |
| cos(x) | -sin(x) | sin(x) + C |
Applications of the Antiderivative

The antiderivative of sin(x) has numerous applications in various fields, including physics, engineering, and mathematics. In physics, the antiderivative of sin(x) is used to model the motion of objects, such as simple harmonic motion. In engineering, the antiderivative of sin(x) is used to design and analyze systems, such as electrical circuits and mechanical systems. In mathematics, the antiderivative of sin(x) is used to solve problems in calculus, such as finding the area under curves and solving differential equations.
Technical Specifications
The antiderivative of sin(x) can be specified technically as ∫sin(x) dx = -cos(x) + C, where C is the constant of integration. The domain of the antiderivative is all real numbers, and the range is all real numbers. The antiderivative of sin(x) is a continuous and differentiable function, making it an ideal candidate for integration.
What is the antiderivative of sin(x)?
+The antiderivative of sin(x) is -cos(x) + C, where C is the constant of integration.
What is the geometric interpretation of the antiderivative of sin(x)?
+The antiderivative of sin(x) can be visualized as the area under the sine curve, which is equal to the negative of the area under the cosine curve.
What are the applications of the antiderivative of sin(x)?
+The antiderivative of sin(x) has numerous applications in physics, engineering, and mathematics, including modeling the motion of objects, designing and analyzing systems, and solving problems in calculus.
In conclusion, the antiderivative of sin(x) is a fundamental concept in calculus that has numerous applications in various fields. Understanding the properties and behavior of this function is essential for solving problems in physics, engineering, and mathematics. The antiderivative of sin(x) can be derived using the fact that the derivative of the cosine function is equal to -sin(x), and it can be interpreted geometrically as the area under the sine curve. With its numerous applications and technical specifications, the antiderivative of sin(x) is a powerful tool for solving problems in calculus and beyond.