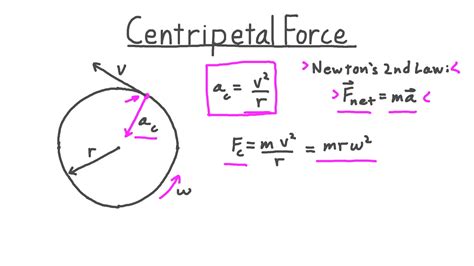
The concept of angular speed is a fundamental aspect of rotational motion in physics. It is a measure of how fast an object is rotating or revolving around a fixed point. The angular speed formula is a crucial tool for calculating this quantity, and it has numerous applications in various fields, including engineering, astronomy, and sports. In this article, we will delve into the details of the angular speed formula, its derivation, and its practical applications.
Key Points
- The angular speed formula is given by ω = Δθ / Δt, where ω is the angular speed, Δθ is the change in angular displacement, and Δt is the time interval.
- Angular speed is typically measured in units of radians per second (rad/s) or degrees per second (deg/s).
- The angular speed formula is a vector quantity, and its direction is perpendicular to the plane of rotation.
- The formula has numerous applications in physics, engineering, and astronomy, including the calculation of rotational kinematics, dynamics, and energy.
- Understanding the angular speed formula is essential for designing and optimizing rotational systems, such as gears, motors, and turbines.
Derivation of the Angular Speed Formula

The angular speed formula can be derived from the definition of angular displacement and the concept of average speed. Angular displacement (Δθ) is the change in the angular position of an object over a given time interval (Δt). The average angular speed (ω) is defined as the total angular displacement divided by the time interval: ω = Δθ / Δt. This formula provides a simple and intuitive way to calculate the angular speed of an object.
Mathematical Representation
The angular speed formula can be mathematically represented as ω = dθ/dt, where dθ is the infinitesimal change in angular displacement and dt is the infinitesimal time interval. This representation is useful for calculating the instantaneous angular speed of an object. In polar coordinates, the angular speed can be represented as ω = r × v / |r|^2, where r is the position vector, v is the velocity vector, and |r| is the magnitude of the position vector.
| Physical Quantity | Symbol | Unit |
|---|---|---|
| Angular speed | ω | rad/s |
| Angular displacement | Δθ | rad |
| Time interval | Δt | s |
Practical Applications

The angular speed formula has numerous practical applications in various fields, including physics, engineering, and astronomy. In physics, it is used to calculate the rotational kinematics and dynamics of objects, such as the motion of a pendulum or the rotation of a wheel. In engineering, it is used to design and optimize rotational systems, such as gears, motors, and turbines. In astronomy, it is used to calculate the orbital periods of celestial bodies and the rotation rates of stars and planets.
Real-World Examples
Some real-world examples of the angular speed formula in action include the design of helicopter rotors, the calculation of the rotation rate of a CD player, and the determination of the orbital period of a satellite. In each of these cases, the angular speed formula provides a critical tool for understanding and optimizing the rotational motion of the system.
What is the unit of angular speed?
+The unit of angular speed is typically measured in radians per second (rad/s) or degrees per second (deg/s).
How is angular speed calculated?
+Angular speed is calculated using the formula ω = Δθ / Δt, where ω is the angular speed, Δθ is the change in angular displacement, and Δt is the time interval.
What are some practical applications of the angular speed formula?
+The angular speed formula has numerous practical applications in physics, engineering, and astronomy, including the design of rotational systems, the calculation of rotational kinematics and dynamics, and the determination of orbital periods.
In conclusion, the angular speed formula is a fundamental concept in physics and engineering, and it has numerous applications in the design and optimization of rotational systems. Understanding the formula and its underlying principles is essential for working with rotational motion and designing efficient systems. By applying the angular speed formula, engineers and physicists can calculate the rotational kinematics and dynamics of objects, design and optimize rotational systems, and determine the orbital periods of celestial bodies.