The probability addition rule is a fundamental concept in statistics and probability theory, allowing us to calculate the probability of multiple events occurring. This rule is essential in understanding how to combine probabilities of different events to determine the overall likelihood of an outcome. In this article, we will explore the five ways the probability addition rule works, providing a comprehensive understanding of its applications and implications.
Key Points
- The probability addition rule is used to calculate the probability of at least one event occurring.
- It is essential to understand the concept of mutually exclusive and non-mutually exclusive events.
- The rule can be applied in various fields, including insurance, finance, and engineering.
- Calculating the probability of independent and dependent events requires different approaches.
- Understanding the probability addition rule is crucial for making informed decisions in uncertain situations.
Understanding the Probability Addition Rule
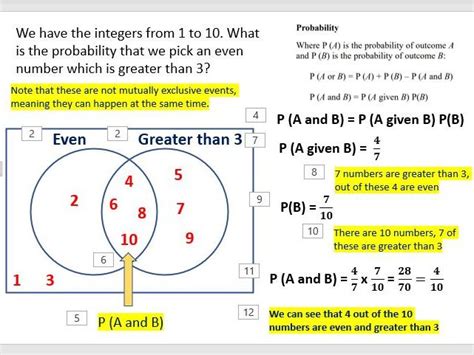
The probability addition rule states that the probability of at least one event occurring is equal to 1 minus the probability of none of the events occurring. Mathematically, this can be represented as P(A ∪ B) = P(A) + P(B) - P(A ∩ B), where P(A) and P(B) are the probabilities of events A and B, respectively, and P(A ∩ B) is the probability of both events occurring. This rule is essential in understanding how to combine probabilities of different events to determine the overall likelihood of an outcome.
Application in Mutually Exclusive Events
Mutually exclusive events are those that cannot occur simultaneously. For example, flipping a coin can result in either heads or tails, but not both. In such cases, the probability addition rule can be simplified to P(A ∪ B) = P(A) + P(B), as the probability of both events occurring is zero. This is a straightforward application of the rule, and it is widely used in various fields, including insurance and finance.
| Event | Probability |
|---|---|
| Heads | 0.5 |
| Tails | 0.5 |

Non-Mutually Exclusive Events and the Probability Addition Rule
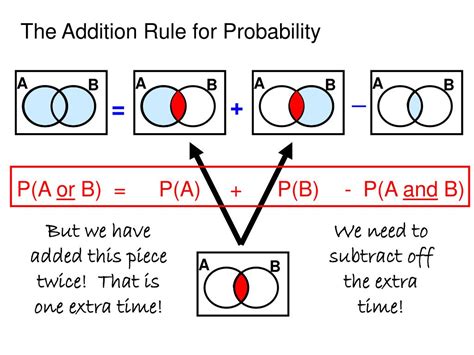
Non-mutually exclusive events are those that can occur simultaneously. For example, a person can be both a smoker and a drinker. In such cases, the probability addition rule must take into account the probability of both events occurring, which can be calculated using the formula P(A ∪ B) = P(A) + P(B) - P(A ∩ B). This requires a more nuanced understanding of the events and their relationships.
Calculating the Probability of Independent Events
Independent events are those where the occurrence of one event does not affect the probability of the other event. For example, flipping a coin twice, where the outcome of the first flip does not affect the outcome of the second flip. In such cases, the probability of both events occurring can be calculated by multiplying the probabilities of the individual events, i.e., P(A ∩ B) = P(A) × P(B). This is a critical concept in understanding how to calculate the probability of complex events.
Dependent Events and the Probability Addition Rule
Dependent events are those where the occurrence of one event affects the probability of the other event. For example, drawing a card from a deck, where the probability of drawing a specific card changes after each draw. In such cases, the probability of both events occurring must take into account the conditional probability of the second event given that the first event has occurred, i.e., P(A ∩ B) = P(A) × P(B|A). This requires a deep understanding of the relationships between the events and how they impact each other.
What is the difference between mutually exclusive and non-mutually exclusive events?
+Mutually exclusive events are those that cannot occur simultaneously, whereas non-mutually exclusive events can occur simultaneously. This distinction is crucial in applying the probability addition rule, as it affects the calculation of the overall probability.
How do you calculate the probability of independent events?
+The probability of independent events can be calculated by multiplying the probabilities of the individual events, i.e., P(A ∩ B) = P(A) × P(B). This is a fundamental concept in probability theory and is widely used in various fields.
What is the importance of understanding the probability addition rule?
+Understanding the probability addition rule is crucial for making informed decisions in uncertain situations. It allows us to calculate the probability of complex events and make predictions about future outcomes. This is essential in fields such as insurance, finance, and engineering, where accurate probability calculations can have significant implications.
In conclusion, the probability addition rule is a powerful tool for calculating the probability of multiple events occurring. By understanding the different ways this rule works, including its application in mutually exclusive and non-mutually exclusive events, independent and dependent events, we can gain a deeper insight into the world of probability and make more informed decisions in uncertain situations. Whether you are an expert in statistics or just starting to explore the world of probability, the probability addition rule is an essential concept to grasp, and its applications are diverse and far-reaching.