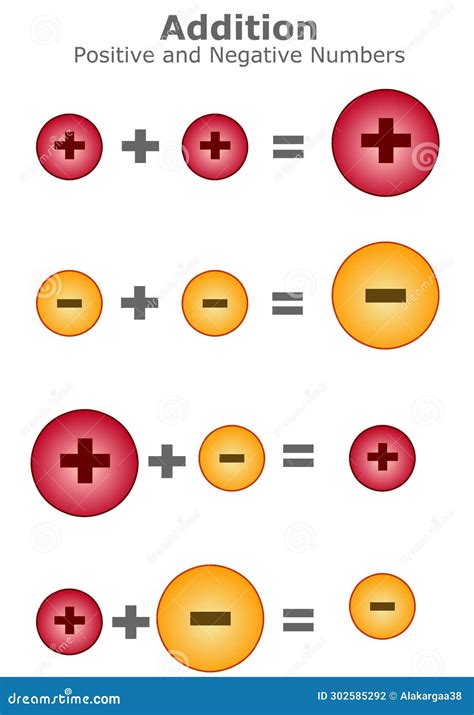When it comes to dealing with negative numbers in mathematics, many individuals find themselves struggling to comprehend the concepts of addition and subtraction. Negative numbers are often viewed as complex and intimidating, but with a solid understanding of the underlying principles, these operations can become second nature. In this article, we will delve into the world of negative numbers, exploring the rules and techniques for adding and subtracting them with ease.
Understanding Negative Numbers

Negative numbers are essentially the opposite of positive numbers. They can be thought of as debts or deficiencies, whereas positive numbers represent quantities or amounts. The concept of negative numbers is rooted in the number line, where positive numbers extend to the right and negative numbers extend to the left. The number zero serves as the midpoint, separating the positive and negative realms. To truly grasp the concept of negative numbers, it’s essential to understand the number line and how numbers interact with one another.
Key Points
- Negative numbers are the opposite of positive numbers and can be thought of as debts or deficiencies.
- The number line is a visual representation of numbers, with positive numbers extending to the right and negative numbers extending to the left.
- Zero serves as the midpoint between positive and negative numbers.
- Understanding the number line is crucial for working with negative numbers.
- Adding and subtracting negative numbers requires a solid grasp of the underlying principles.
Adding Negative Numbers
When adding negative numbers, it’s essential to remember that you are essentially combining debts or deficiencies. The rules for adding negative numbers are as follows: when adding two negative numbers, the result is the sum of the two numbers, but with a negative sign. For example, -3 + (-5) = -8. On the other hand, when adding a negative number to a positive number, you need to subtract the absolute value of the negative number from the positive number. For instance, 7 + (-3) = 4.
| Operation | Example | Result |
|---|---|---|
| Adding two negative numbers | -3 + (-5) | -8 |
| Adding a negative number to a positive number | 7 + (-3) | 4 |
Subtracting Negative Numbers

Subtracting negative numbers can be a bit more complex, but with practice, it becomes straightforward. When subtracting a negative number from another number, you are essentially adding the opposite of the negative number. The rules for subtracting negative numbers are as follows: when subtracting a negative number from a positive number, add the absolute value of the negative number to the positive number. For example, 10 - (-3) = 13. On the other hand, when subtracting a negative number from another negative number, you need to add the absolute value of the negative number being subtracted to the other negative number, but keep the negative sign. For instance, -5 - (-3) = -2.
Real-World Applications of Negative Numbers
Negative numbers have numerous real-world applications, from finance and accounting to physics and engineering. In finance, negative numbers can represent debts or losses, while in physics, they can denote opposite directions or quantities. Understanding how to work with negative numbers is essential for making informed decisions and solving complex problems in various fields.
In conclusion, adding and subtracting negative numbers is a matter of understanding the underlying principles and rules. By grasping the concept of the number line, paying attention to signs, and applying the rules for adding and subtracting negative numbers, you can become proficient in working with these types of numbers. Remember, practice makes perfect, so be sure to practice adding and subtracting negative numbers regularly to solidify your understanding.
What is the difference between adding and subtracting negative numbers?
+When adding negative numbers, you are essentially combining debts or deficiencies. When subtracting negative numbers, you are adding the opposite of the negative number. The key difference lies in the signs and the operations involved.
How do I determine the sign of the result when adding or subtracting negative numbers?
+The sign of the result depends on the signs of the numbers involved in the operation. When adding two negative numbers, the result is always negative. When adding a negative number to a positive number, the result is positive if the positive number is larger, and negative if the negative number is larger. When subtracting a negative number from a positive number, the result is always positive. When subtracting a negative number from another negative number, the result is negative.
What are some real-world applications of negative numbers?
+Negative numbers have numerous real-world applications, including finance, accounting, physics, and engineering. They can represent debts, losses, opposite directions, or quantities, making them essential for making informed decisions and solving complex problems.