Adding fractions is a fundamental concept in mathematics that can be approached in various ways, depending on the nature of the fractions involved. When dealing with fractions, it's essential to understand the different methods that can be used to add them together. In this article, we will explore five ways to add fractions, including adding fractions with like denominators, adding fractions with unlike denominators, using the least common multiple (LCM), using the least common denominator (LCD), and adding mixed numbers.
Key Points
- Understanding the concept of like and unlike denominators is crucial for adding fractions.
- The least common multiple (LCM) and least common denominator (LCD) are essential for adding fractions with unlike denominators.
- Adding mixed numbers involves converting the mixed numbers to improper fractions and then adding them together.
- Visual aids such as number lines and fraction strips can help students understand the concept of adding fractions.
- Real-world applications of adding fractions include cooking, measurement, and finance.
Adding Fractions with Like Denominators

Adding fractions with like denominators is a straightforward process. When the denominators are the same, we can simply add the numerators together and keep the same denominator. For example, to add 1⁄4 and 1⁄4, we can add the numerators (1 + 1) and keep the same denominator (4), resulting in 2⁄4, which can be simplified to 1⁄2.
Example: Adding 1⁄4 and 1⁄4
To add 1⁄4 and 1⁄4, we can follow these steps:
- Check if the denominators are the same (4 = 4).
- Add the numerators together (1 + 1 = 2).
- Keep the same denominator (4).
- Simplify the fraction, if possible (2⁄4 = 1⁄2).
| Fraction | Numerator | Denominator |
|---|---|---|
| 1/4 | 1 | 4 |
| 1/4 | 1 | 4 |
| 1/2 | 2 | 4 |
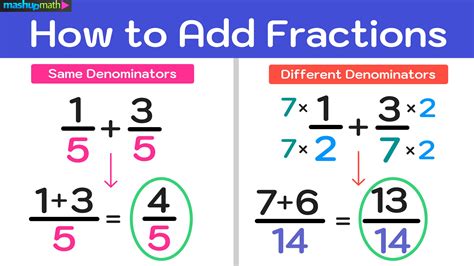
Adding Fractions with Unlike Denominators

Adding fractions with unlike denominators requires finding a common denominator. One way to do this is to use the least common multiple (LCM) of the two denominators. For example, to add 1⁄4 and 1⁄6, we need to find the LCM of 4 and 6, which is 12. We can then convert both fractions to have a denominator of 12 and add them together.
Example: Adding 1⁄4 and 1⁄6
To add 1⁄4 and 1⁄6, we can follow these steps:
- Find the LCM of the denominators (4 and 6), which is 12.
- Convert both fractions to have a denominator of 12 (1⁄4 = 3⁄12 and 1⁄6 = 2⁄12).
- Add the numerators together (3 + 2 = 5).
- Keep the same denominator (12).
- Simplify the fraction, if possible (5⁄12).
| Fraction | Numerator | Denominator |
|---|---|---|
| 1/4 | 1 | 4 |
| 1/6 | 1 | 6 |
| 5/12 | 5 | 12 |
Using the Least Common Multiple (LCM)
The LCM is the smallest multiple that is exactly divisible by each of the numbers. To find the LCM of two numbers, we can list the multiples of each number and find the smallest multiple that is common to both lists. For example, to find the LCM of 4 and 6, we can list the multiples of 4 (4, 8, 12, 16,…) and the multiples of 6 (6, 12, 18, 24,…). The smallest multiple that is common to both lists is 12, which is the LCM of 4 and 6.
Example: Finding the LCM of 4 and 6
To find the LCM of 4 and 6, we can follow these steps:
- List the multiples of 4 (4, 8, 12, 16,…).
- List the multiples of 6 (6, 12, 18, 24,…).
- Find the smallest multiple that is common to both lists (12).
| Number | Multiples |
|---|---|
| 4 | 4, 8, 12, 16,... |
| 6 | 6, 12, 18, 24,... |
| LCM | 12 |
Using the Least Common Denominator (LCD)
The LCD is the smallest common multiple of the denominators. To find the LCD, we can use the same method as finding the LCM. For example, to find the LCD of 1⁄4 and 1⁄6, we can find the LCM of 4 and 6, which is 12. We can then convert both fractions to have a denominator of 12 and add them together.
Example: Finding the LCD of 1⁄4 and 1⁄6
To find the LCD of 1⁄4 and 1⁄6, we can follow these steps:
- Find the LCM of the denominators (4 and 6), which is 12.
- Convert both fractions to have a denominator of 12 (1⁄4 = 3⁄12 and 1⁄6 = 2⁄12).
- Add the numerators together (3 + 2 = 5).
- Keep the same denominator (12).
- Simplify the fraction, if possible (5⁄12).
| Fraction | Numerator | Denominator |
|---|---|---|
| 1/4 | 1 | 4 |
| 1/6 | 1 | 6 |
| 5/12 | 5 | 12 |
Adding Mixed Numbers

Adding mixed numbers involves converting the mixed numbers to improper fractions and then adding them together. For example, to add 2 1⁄4 and 1 1⁄6, we can convert both mixed numbers to improper fractions (2 1⁄4 = 9⁄4 and 1 1⁄6 = 7⁄6) and then find the LCD, which is 12. We can then convert both fractions to have a denominator of 12 (9⁄4 = 27⁄12 and 7⁄6 = 14⁄12) and add them together.
Example: Adding 2 1⁄4 and 1 1⁄6
To add 2 1⁄4 and 1 1⁄6, we can follow these steps:
- Convert both mixed numbers to improper fractions (2 1⁄4 = 9⁄4 and 1 1⁄6 = 7⁄6).
- Find the LCD of the denominators (4 and 6), which is 12.
- Convert both fractions to have a denominator of 12 (9⁄4 = 27⁄12 and 7⁄6 = 14⁄12).
- Add the numerators together (27 + 14 = 41).
- Keep the same denominator (12).
- Simplify the fraction, if possible (41⁄12 = 3 5⁄12).
| Fraction | Numerator | Denominator |
|---|---|---|
| 2 1/4 | 9 | 4 |
| 1 1/6 | 7 | 6 |
| 3 5/12 | 41 | 12 |
What is the difference between adding fractions with like denominators and unlike denominators?
+When adding fractions with like denominators, we can simply add the numerators together and keep the same denominator. However, when adding fractions with unlike denominators, we need to find a common denominator, such as the least common multiple (LCM) or least common denominator (LCD), before adding the numerators together.
How do I find the least common multiple (LCM) of two numbers?
+To find the LCM of two numbers, we can list the multiples of each number and find the smallest multiple that is common to both lists. For example, to find the LCM of 4 and 6, we can list the multiples of 4 (4, 8, 12, 16,…) and the multiples of 6 (6, 12, 18, 24,…). The smallest multiple that is common to both lists is 12, which is the LCM of 4 and 6.
Can I add mixed numbers directly without converting them to improper fractions?
+No, it’s not recommended to add mixed numbers directly without converting them to improper fractions. This is because mixed numbers have a combination of a whole number and a fraction, and adding them directly can lead to errors. Instead, we should convert the mixed numbers to improper fractions, find the LCD, and then add the numerators together.



