Dividing fractions by whole numbers can seem intimidating at first, but it's actually a straightforward process. To divide 4/5 by 2, we need to follow a simple rule: when dividing a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number. In this case, the reciprocal of 2 is 1/2. So, to divide 4/5 by 2, we multiply 4/5 by 1/2.
Understanding the Concept
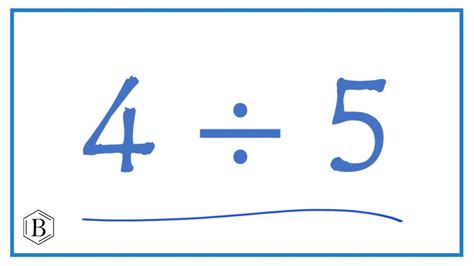
The concept of dividing fractions by whole numbers is based on the idea of multiplying by the reciprocal. The reciprocal of a number is 1 divided by that number. For whole numbers, the reciprocal is simply 1 divided by the number itself. For example, the reciprocal of 3 is 1⁄3, the reciprocal of 4 is 1⁄4, and so on. When we multiply a fraction by the reciprocal of a whole number, we are essentially dividing the fraction by that whole number.
Applying the Rule
To apply this rule to our problem, we multiply 4⁄5 by 1⁄2. When multiplying fractions, we multiply the numerators (the numbers on top) together and the denominators (the numbers on the bottom) together. So, multiplying 4⁄5 by 1⁄2 gives us (4*1)/(5*2) = 4⁄10.
| Operation | Result |
|---|---|
| Multiplying 4/5 by 1/2 | 4/10 |
| Simplifying 4/10 | 2/5 |

Simplifying the Result

Simplifying fractions is an important step in making them easier to understand and work with. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both numbers by this GCD. In the case of 4⁄10, the GCD of 4 and 10 is 2. Dividing both 4 and 10 by 2 gives us 2⁄5, which is the simplified form of 4⁄10.
Key Points
- To divide a fraction by a whole number, multiply the fraction by the reciprocal of the whole number.
- The reciprocal of a whole number is 1 divided by that number.
- Multiplying fractions involves multiplying the numerators together and the denominators together.
- Fractions can often be simplified by dividing both the numerator and the denominator by their greatest common divisor.
- Simplifying fractions makes them easier to work with and understand.
Real-World Applications
Understanding how to divide fractions by whole numbers has numerous real-world applications. For instance, in cooking, if a recipe calls for 4⁄5 of a cup of flour but you want to make half the recipe, you would need to divide 4⁄5 by 2, resulting in 2⁄5 of a cup of flour. This basic mathematical operation is crucial in various aspects of life, from science and engineering to everyday problem-solving.
In conclusion, dividing 4/5 by 2 involves a simple mathematical operation: multiplying 4/5 by the reciprocal of 2, which is 1/2, resulting in 4/10, and then simplifying 4/10 to 2/5. This process demonstrates the importance of understanding the rules of fraction operations and how they apply to real-world scenarios.
What is the rule for dividing a fraction by a whole number?
+To divide a fraction by a whole number, you multiply the fraction by the reciprocal of the whole number.
How do you simplify a fraction?
+You simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor.
What is the result of dividing 4⁄5 by 2?
+The result of dividing 4⁄5 by 2 is 2⁄5.



