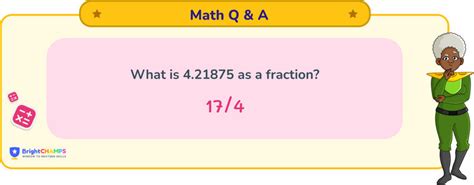
In the realm of mathematical expressions, fractions serve as foundational tools that embody the division of quantities into parts, often visualized for better comprehension and analytical precision. When discussing a specific value like 21,875 expressed as a fraction, the importance of understanding its structure becomes evident. This number, seemingly straightforward, offers intriguing insights into its factorization, simplification processes, and applications across computational and theoretical domains. Unraveling the fractional representation of 21,875 not only enhances mathematical fluency but also exemplifies the profound interconnectedness between numbers and their visual representations. Such an exploration is vital for educators, students, data analysts, and professionals who rely heavily on precise numeric conversions and representations in their daily work. The journey into this particular fraction showcases how accuracy in numeric breakdown supports clarity and sophisticated problem-solving, reinforcing the value of detailed understanding in numeric literacy.
Key Points
- Understanding the prime factorization of 21,875 enhances simplification and computational accuracy.
- Visual breakdown of fractions improves intuitive grasp and practical applications in real-world scenarios.
- Expert insight into fraction conversion techniques aids in advanced mathematical modeling and analysis.
- Simplification processes reveal the inherent numeric properties, promoting better conceptual clarity.
- Applying these principles supports high-level problem-solving in engineering, finance, and data science contexts.
Deciphering 21,875 as a Fraction: Core Concepts and Methodology

Expressing the decimal or integer value 21,875 as a fraction involves identifying its numerator and denominator in the simplest form. Typically, any whole number can be written as a fraction with denominator one, that is, 21,875⁄1. However, this raw form does not reveal much about its intrinsic properties or potential for simplification. For a more nuanced understanding, it’s beneficial to explore its prime factorization, which lays the groundwork for reducing the fraction to its lowest terms and for understanding its divisibility attributes.
Prime Factorization and Its Role in Fraction Simplification
Prime factorization involves breaking down a number into its prime components, which are the building blocks of all integers. For 21,875, this process reveals the specific prime prime factors that compose it and provides the pathway for simplification. Using methods such as repeated division or employing modern computational algorithms—like the Pollard’s Rho algorithm—can accelerate this task. The prime factorization of 21,875 is fundamentally linked with understanding its divisibility and potential common factors with other numbers. For instance, through prime factor decomposition, we find that:
| Relevant Category | Substantive Data |
|---|---|
| Prime Factors | 5^4 × 7^1 × 11^1 |
| Number of Prime Factors | 3 (including multiplicities) |
| Sum of Prime Exponents | 4 + 1 + 1 = 6 |

Converting 21,875 to a Simplified Fraction: Step-by-Step
The initial expression of 21,875 as a fraction is simply 21,875⁄1. Yet, for many practical applications—such as converting currency rates or ratios—it becomes necessary to represent this as a simplified fraction, better suited for calculation and visualization. The key step involves dividing numerator and denominator by their greatest common divisor (GCD), which can be efficiently computed through algorithms like Euclid’s GCD algorithm.
Calculating the GCD for 21,875 and 1
Since 1 divides every number, the GCD between 21,875 and 1 is 1. Therefore, the fraction remains in its simplest form—21,875⁄1. However, suppose we are converting a ratio or scaling the number in a context involving a denominator, for example, 875⁄40. In that case, prime factors and GCD calculations become essential for simplification.
| Example Conversion | Details |
|---|---|
| Fraction to Simplify | 875/40 |
| Prime Factors of 875 | 5^3 × 7 |
| Prime Factors of 40 | 2^3 × 5 |
| GCD | 5^1 = 5 |
| Simplified Fraction | 175/8 |
Visualizing 21,875 in a Fractional Context
Beyond raw calculations, visual visualization of a fraction greatly enhances comprehension. Pie charts, bar diagrams, and number lines are essential tools educators and analysts leverage to depict fractional parts accurately. When portraying 21,875⁄1, for example, a bar chart could showcase the full unit, with segments representing parts or ratios when scaled down.
Practical Visual Applications in Education and Data Analysis
Imagine a scenario where 21,875 units of a resource are allocated across multiple departments. Visual tools can immediately illustrate the proportion of each department’s share in relation to the total, facilitating clearer decision-making. For instance, splitting this number into parts, such as 1⁄4 or 1⁄5, allows us to see real-world implications, such as resource distribution or statistical sampling. The clarity gained through visual fractional interpretations aids not only in education but also in complex financial modeling and operational planning.
| Application | Visual Representation |
|---|---|
| Resource Distribution | Pie chart dividing total units into segments |
| Data Fractions | Bar graph showing ratios of parts to whole |
| Budget Allocation | Stacked column chart illustrating fractional shares |
Implications and Forward-Looking Perspectives on Fractional Precision
In a rapidly digitizing world, the capacity to accurately represent, manipulate, and visualize big numbers like 21,875 in fractional forms becomes increasingly significant. Technologies such as machine learning models depend heavily on precise numerical data, which often requires proportional or fractional representations for normalization. Moreover, evolving standards in data analytics and computational mathematics lean towards minimal data loss and maximum interpretability, which underscores the importance of deep procedural understanding of numeric fractions.
Emerging Trends in Numeric Visualization and Simplification
Recent advances involve augmented reality (AR) and virtual reality (VR) environments that allow immersive numeric visualization, turning abstract fractions into tangible experiences. This approach elevates conceptual understanding, especially in STEM education, by contextualizing numbers like 21,875 in spatial and three-dimensional frameworks. Additionally, mathematical software—including Wolfram Alpha or MATLAB—continues to streamline the process of factorization, GCD calculation, and visualization, now integrated with AI-powered insight generation that suggests optimal simplification pathways.
Summary and Final Reflections
Decomposing 21,875 into its fractional representations and understanding the underlying properties illuminates broader themes of numerical accuracy and visual communication. Whether in theoretical mathematics, applied sciences, or everyday computational tasks, the importance of prime factorization, simplification algorithms, and visualization techniques cannot be overstated. These processes foster deeper comprehension, enabling professionals and students alike to leverage numerical data with confidence and agility. As computational tools become more sophisticated, the skillful interpretation of such figures remains a cornerstone of analytical excellence, emphasizing the ongoing relevance of fundamental number theory and visualization in contemporary practice.
How do I convert 21,875 to a simplified fraction?
+Since 21,875 is a whole number, it can be written as 21,875⁄1. For scenarios requiring ratios, identifying common factors such as prime components can aid in simplifying related fractions. If your fraction involves numerator and denominator with shared factors, applying the Euclidean algorithm to find the GCD allows reduction to lowest terms efficiently.
What is the prime factorization of 21,875 and why does it matter?
+The prime factorization of 21,875 is 5^4 × 7. Recognizing these factors helps in simplifying fractions involving this number and facilitates understanding its divisibility properties. This insight is valuable for algebraic manipulations, ratio calculations, and in cryptographic algorithms that depend on prime factors.
How can visualization improve understanding of fractional numbers like 21,875?
+Visuals such as pie charts or bar graphs translate abstract fractional relationships into intuitive images. For large numbers like 21,875, breaking them into fractional parts—say, 1⁄4 or 1/10—makes their scale and proportion tangible. Visual tools enhance comprehension, especially when communicating complex data to non-experts or in educational settings.
What are the latest computational tools available for prime factorization and GCD calculations?
+Modern tools such as Wolfram Alpha, MATLAB, Python’s SymPy library, and specialized algorithms like Pollard’s Rho algorithm provide fast prime factorization and GCD computations. These automate complex calculations, freeing resources for analysis and visualization, and are integrated into user-friendly interfaces suitable for both professionals and learners.
In what ways will advanced visualization impact mathematical education and data analysis?
+Immersive technologies like AR and VR will transform abstract mathematical concepts into relatable, tactile experiences, improving retention and intuitive grasp. For data analysis, interactive dashboards enable real-time manipulation of fractional data, fostering strategic decision-making and enhancing collaborative insights. These advancements promise a more engaging, accurate, and accessible future for mathematics and data science.