Calculating percentages is a fundamental mathematical operation that is commonly used in various aspects of life, including finance, commerce, and daily transactions. One of the most frequent calculations involves finding a percentage of a given number. For instance, calculating 20% of 70 is a straightforward process that can be approached in multiple ways, catering to different learning styles and preferences. Here are five distinct methods to calculate 20% of 70, each offering a unique perspective on how to arrive at the solution.
Method 1: Using the Percentage Formula
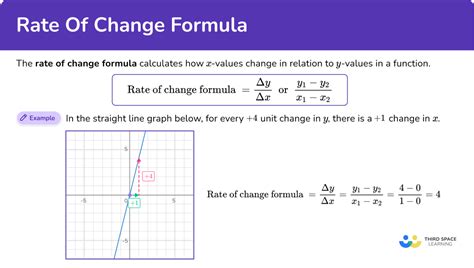
The most direct method to calculate 20% of 70 involves using the percentage formula. The formula for finding a percentage of a number is: (percentage / 100) * number. Applying this formula to our problem: (20 / 100) * 70. Simplifying this, we get 0.20 * 70 = 14. Therefore, 20% of 70 is 14.
Breaking Down the Calculation
This method is straightforward and relies on basic arithmetic operations. It’s essential to understand that the percentage sign (%) means “out of 100,” which is why we divide by 100 to convert the percentage to a decimal before multiplying by the number in question.
Method 2: Converting Percentage to Decimal
Another approach is to first convert the percentage to a decimal and then multiply by the number. To convert 20% to a decimal, we divide by 100: 20 / 100 = 0.20. Then, we multiply this decimal by 70: 0.20 * 70 = 14. This method reinforces the concept that percentages can be easily converted to decimals for calculation purposes.
Understanding Decimal Conversion
Converting percentages to decimals is a crucial step in many mathematical operations. It simplifies calculations and makes them more intuitive. In this case, converting 20% to 0.20 allows for a straightforward multiplication to find 20% of 70.
Method 3: Using Fractions
A more traditional or alternative approach involves using fractions. Since 20% can be represented as 20⁄100, which simplifies to 1⁄5, we can find 20% of 70 by multiplying 70 by 1⁄5. This calculation is: 70 * (1⁄5) = 70 / 5 = 14. This method is useful for those who prefer working with fractions or need to understand the conceptual basis of percentages.
Fractional Representation
Representing percentages as fractions can provide a deeper understanding of the proportional relationships involved. In this example, seeing 20% as 1⁄5 of the whole helps in visualizing the proportion that 20% represents of 70.
Method 4: Estimation and Adjustment
For a more intuitive or estimation-based approach, one can start with an easy percentage calculation, like 10% of 70, which is 7. Then, doubling this gives 20% of 70, since 20% is twice 10%. Therefore, 2 * 7 = 14. This method is useful for quick estimations or when a calculator is not available.
Estimation Techniques
Estimation techniques are valuable in real-world applications where exact calculations might not be immediately necessary or possible. By breaking down percentages into more manageable parts, like using 10% as a base, one can quickly estimate percentages of numbers.
Method 5: Using a Calculator
The most straightforward method, especially for those with access to a calculator, is to simply input the calculation. Most calculators allow you to input percentages directly, so typing “20% of 70” or “0.20 * 70” will yield the result 14. This method is the quickest but does rely on having a calculator or computer available.
Calculator Usage
Calculators and computers have made mathematical operations incredibly accessible. For percentage calculations, using a calculator can save time and reduce the chance of error, especially when dealing with more complex percentages or large numbers.
Key Points
- There are multiple methods to calculate percentages, including using the percentage formula, converting percentages to decimals, using fractions, estimation techniques, and calculators.
- Understanding the conceptual basis of percentages, such as converting between percentages, decimals, and fractions, is crucial for flexible mathematical thinking.
- Each method has its own advantages and may be preferred in different situations or by different individuals.
- Practice with various methods can enhance mathematical fluency and problem-solving abilities.
- Calculators and digital tools can expedite calculations but understanding the underlying mathematical principles is essential for a deep comprehension of percentage calculations.
| Method | Description | Calculation |
|---|---|---|
| Percentage Formula | Using the formula (percentage / 100) * number | (20 / 100) * 70 = 14 |
| Decimal Conversion | Converting percentage to decimal and then multiplying | 0.20 * 70 = 14 |
| Fractions | Representing percentage as a fraction and multiplying | 70 * (1/5) = 14 |
| Estimation | Estimating based on easier percentages and adjusting | 2 * 7 = 14 |
| Calculator | Directly calculating using a calculator | 20% of 70 = 14 |
What is the easiest way to calculate 20% of a number?
+The easiest way often involves converting the percentage to a decimal and then multiplying by the number. For 20%, this means multiplying the number by 0.20.
How do I convert a percentage to a decimal?
+To convert a percentage to a decimal, divide the percentage by 100. For example, 20% becomes 0.20 when converted to a decimal.
Can I use fractions to calculate percentages?
+Yes, percentages can be represented as fractions. For instance, 20% is equivalent to 1/5. This can be useful for certain calculations or for understanding the proportional relationship.
Meta Description: Discover five straightforward methods to calculate 20% of 70, including using the percentage formula, converting to decimals, working with fractions, estimation techniques, and calculator usage, each offering a unique approach to finding the solution.