The Taylor series is a fundamental concept in calculus, allowing us to represent complex functions as infinite sums of simpler terms. One of the most well-known and widely used Taylor series expansions is the expansion of 1 / (1 + x), which is a crucial tool in various mathematical and scientific applications. In this article, we will delve into the world of Taylor series, explore the 1 / (1 + x) expansion, and provide a comprehensive understanding of this essential mathematical concept.
Key Points
- The Taylor series expansion of 1 / (1 + x) is a geometric series that converges to the original function for |x| < 1.
- The expansion is given by 1 - x + x^2 - x^3 +..., which can be derived using the binomial theorem or other methods.
- The Taylor series expansion of 1 / (1 + x) has numerous applications in mathematics, physics, engineering, and other fields, including calculus, algebra, and numerical analysis.
- The convergence of the series is guaranteed by the ratio test, which shows that the series converges absolutely for |x| < 1 and diverges for |x| ≥ 1.
- The 1 / (1 + x) expansion is a special case of the more general binomial series expansion, which can be used to represent a wide range of functions.
Introduction to Taylor Series
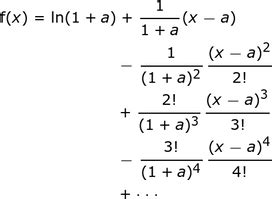
Taylor series are a way to represent a function as an infinite sum of terms, each of which is a power of the variable x. The general form of a Taylor series is given by f(x) = a0 + a1x + a2x^2 +…, where the coefficients a0, a1, a2,… are determined by the function f(x) and the point around which the series is expanded. The Taylor series expansion of a function can be used to approximate the function, solve equations, and study the properties of the function.
Derivation of the 1 / (1 + x) Expansion
The Taylor series expansion of 1 / (1 + x) can be derived using the binomial theorem, which states that (1 + x)^n = 1 + nx + n(n-1)x^2⁄2! +… for any real number n. By setting n = -1, we obtain the expansion 1 / (1 + x) = 1 - x + x^2 - x^3 +…, which is valid for |x| < 1. This expansion can also be derived using other methods, such as the use of geometric series or the application of the ratio test.
| Series Expansion | Convergence Interval |
|---|---|
| 1 - x + x^2 - x^3 +... | |x| < 1 |

Properties and Applications of the 1 / (1 + x) Expansion

The 1 / (1 + x) expansion has several important properties and applications. It is a geometric series, which means that each term is obtained by multiplying the previous term by -x. The series converges absolutely for |x| < 1 and diverges for |x| ≥ 1, as shown by the ratio test. The expansion is also a special case of the more general binomial series expansion, which can be used to represent a wide range of functions.
Convergence and Divergence of the Series
The convergence of the 1 / (1 + x) expansion is guaranteed by the ratio test, which states that a series converges absolutely if the limit of the ratio of successive terms is less than 1. For the 1 / (1 + x) expansion, this limit is |x|, which is less than 1 for |x| < 1. Therefore, the series converges absolutely for |x| < 1 and diverges for |x| ≥ 1.
The 1 / (1 + x) expansion has numerous applications in mathematics, physics, engineering, and other fields. It is used to approximate functions, solve equations, and study the properties of functions. The expansion is also a fundamental tool in calculus, where it is used to derive the binomial theorem and other important results.
What is the Taylor series expansion of 1 / (1 + x)?
+The Taylor series expansion of 1 / (1 + x) is 1 - x + x^2 - x^3 +..., which is valid for |x| < 1.
How is the 1 / (1 + x) expansion derived?
+The 1 / (1 + x) expansion can be derived using the binomial theorem, geometric series, or the application of the ratio test.
What are the properties and applications of the 1 / (1 + x) expansion?
+The 1 / (1 + x) expansion is a geometric series that converges absolutely for |x| < 1 and diverges for |x| ≥ 1. It has numerous applications in mathematics, physics, engineering, and other fields, including calculus, algebra, and numerical analysis.
In conclusion, the 1 / (1 + x) expansion is a fundamental tool in calculus and has numerous applications in mathematics, physics, engineering, and other fields. Its derivation, properties, and applications are essential to understanding the significance and utility of this expansion. By mastering the 1 / (1 + x) expansion, students and professionals can gain a deeper appreciation for the power and beauty of calculus and its applications.